Когда происходит изменение знаков в квадратных неравенствах

В математике часто возникают различные задачи, связанные с определением интервалов, в которых удовлетворяются некоторые условия. Для решения таких задач часто используются неравенства, которые позволяют определить множество значений переменной, удовлетворяющих заданному условию. Одним из видов неравенств являются квадратные неравенства, которые имеют вид ax^2 + bx + c < 0 или ax^2 + bx + c > 0.

Важным моментом при решении квадратных неравенств является определение интервалов, на которых знаки в неравенстве меняются. Знание этих интервалов позволяет получить полное представление о решении неравенства и корректно изобразить его на числовой прямой. Когда мы решаем квадратное неравенство, мы ищем значения переменной, которые удовлетворяют неравенству. То есть, мы ищем значения переменной, при которых левая часть неравенства меньше (или больше) нуля.

Определение интервалов, на которых меняется знак квадратного неравенства, можно произвести с помощью анализа графика параболы, которая задает это неравенство. Для этого необходимо найти абсциссы точек пересечения параболы с осью абсцисс. Также можно использовать стандартную форму квадратного неравенства и применять известные правила алгебры, чтобы получить ответ. Главное, запомните, что квадратное неравенство имеет решение на интервале, на котором знак неравенства не изменяется.

Понятие квадратного неравенства

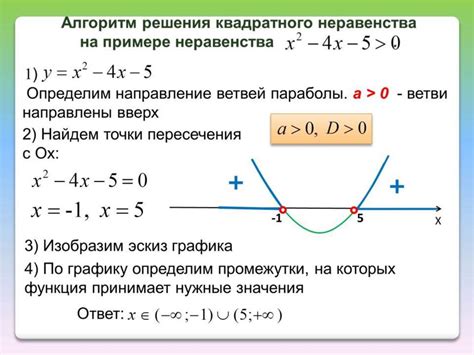
Квадратное неравенство имеет вид:

ax^2 + bx + c > 0

где a, b и c - заданные числа, при этом a ≠ 0, а x - переменная.

Как и в квадратных уравнениях, где присутствуют квадраты переменных, квадратные неравенства могут иметь два корня или быть без корней. Корни определяются методом дискриминанта - значение, полученное в процессе решения квадратного уравнения:

D = b^2 - 4ac

Важно учитывать, что в отличие от уравнений, где корни являются точками их пересечения с осью абсцисс, в случае неравенств корни задают интервалы чисел, удовлетворяющих неравенству. В зависимости от знаков коэффициентов и значения дискриминанта, интервалы могут быть открытыми или закрытыми, а также допустимыми или недопустимыми.

Решая квадратные неравенства, необходимо учитывать правила замены знаков при умножении или делении обеих сторон неравенства на отрицательное число или на число, которое меньше нуля.

Понимание понятия квадратного неравенства позволяет решать и анализировать различные математические проблемы, особенно в области алгебры и геометрии.

Изменение знака при умножении

При умножении обеих частей квадратного неравенства на отрицательное число, знак неравенства изменяется.

Например:

Если у нас есть неравенство a < b, то умножение его обеих частей на отрицательное число, скажем -1, приведет к изменению знака неравенства, и получится новое неравенство -a > -b.

Таким образом, при умножении обеих частей квадратного неравенства на отрицательное число, знак неравенства меняется с меньше на больше или с больше на меньше.

Изменение знака при делении на отрицательное число

При решении квадратных неравенств может возникать ситуация, когда необходимо поделить обе части неравенства на отрицательное число. В таком случае необходимо помнить об особенности изменения знака.

Если мы поделим неравенство на отрицательное число, то необходимо изменить его направление. Например, если у нас есть неравенство -3x < 6 и мы поделим обе части на -3, то получим x > -2. Обратите внимание, что знак неравенства поменялся на противоположный.

Данное правило следует использовать с осторожностью и не забывать проверить полученное неравенство на основе заданного условия. Отсутствие уточнительных условий может привести к неверному ответу при использовании данного правила.

Примеры применения квадратных неравенств

Квадратные неравенства широко применяются в математике и других дисциплинах. Они помогают нам решать множество задач, включая определение интервалов значений переменной, нахождение корней квадратного уравнения и многое другое.

Рассмотрим несколько примеров использования квадратных неравенств:

1. Неравенство вида x^2 > 4: данное неравенство говорит нам о том, что квадрат переменной x больше числа 4. Решим его:
   • При условии x > 2 неравенство выполняется.
   • При условии x < -2 неравенство тоже выполняется.
   • Таким образом, решением данного неравенства является интервал (-∞, -2) ∪ (2, +∞).
2. Неравенство вида x^2 + 3x - 4 < 0: данное неравенство говорит нам о том, что квадрат переменной x плюс 3 умноженное на x минус 4 должно быть меньше нуля. Решим его:
   • При условии x < -4 неравенство не выполняется.
   • При условии x > 1 неравенство тоже не выполняется.
   • Таким образом, решением данного неравенства является интервал (-4, 1).

Это всего лишь два примера использования квадратных неравенств, их применение разнообразно и зависит от конкретной задачи или проблемы. Знание и понимание квадратных неравенств позволяет нам анализировать и решать различные математические и практические задачи.