Проекция - это метод отображения объектов трехмерного пространства на плоскость. Проекцию часто используют в графике, картографии и инженерных расчетах. Существует несколько типов проекций, и одним из наиболее распространенных является проекция в натуральную величину.
Проекция в натуральную величину позволяет сохранить пропорции объектов, отображаемых на плоскости, такими же, как в реальном масштабе. Это означает, что расстояния между точками на плоскости будут соответствовать расстояниям между соответствующими точками в трехмерном пространстве.
Чтобы получить проекцию в натуральную величину, необходимо выбрать точку наблюдения и определить плоскость проекции. При выборе точки наблюдения следует учитывать, что от нее будет зависеть угол обзора и искажения в проекции. Плоскость проекции - это плоскость, на которую будут проецироваться объекты. Она может быть параллельной или перпендикулярной оси зрения.
Что такое прямая проекция и в чем ее суть?

При создании прямой проекции объекты из трехмерного пространства отображаются на плоскости с помощью параллельных линий. Для этого используются различные методы, такие как проекция параллельных линий, проекция центральных линий и другие.
Прямая проекция широко используется в различных областях, где необходимо передавать информацию о трехмерных объектах, например, в архитектуре, инженерии, графике и дизайне. С ее помощью можно создавать точные и наглядные изображения объектов, позволяющие исследовать и рассмотреть их свойства и структуру.
Прямая проекция играет важную роль в создании технических чертежей, планов зданий, разработке промышленных объектов и других сферах деятельности, где требуется графическое представление объектов с сохранением их пропорций и размеров.
Понятие натуральной величины и ее значимость в графических проекциях
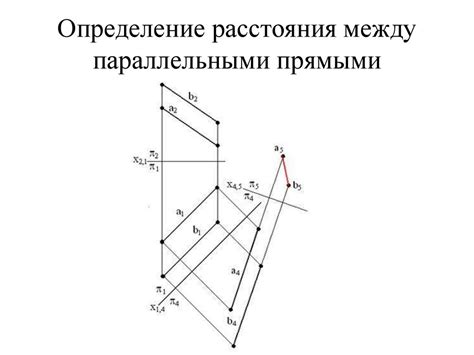
Значимость натуральной величины в графических проекциях состоит в том, что она позволяет создать визуально точное представление о реальных объектах на плоскости. Это особенно важно для работы в областях, где точные измерения имеют критическое значение, таких как архитектура, инженерное дело и географическое картографирование.
Использование натуральной величины в графических проекциях позволяет установить масштаб, который обеспечивает правильное соотношение размеров объектов. Это позволяет точно измерять и сравнивать расстояния, размеры и формы объектов на плоскости. Без использования натуральной величины, результаты графических проекций могут быть искажены и непригодны для детального анализа или использования в практических целях.
Итак, использование натуральной величины в графических проекциях является неотъемлемой частью точности и надежности, необходимых в различных областях деятельности. Это понятие позволяет нам создавать и интерпретировать графические изображения с высокой степенью достоверности и точности, обеспечивая успешное выполнение различных задач и проектов.
Система координат и ее роль в прямой проекции

Прямая проекция – это метод изображения объектов на плоскости, в котором сохраняется соотношение размеров объектов, но не сохраняется их форма и пропорции. Для этого необходимы знания о системе координат.
Система координат обычно состоит из двух осей – горизонтальной (ось X) и вертикальной (ось Y), которые пересекаются в точке (0, 0), называемой началом координат. По этим осям пронумерованы точки, которые могут иметь положительные и отрицательные значений. Такая система координат называется декартовой.
В прямой проекции система координат играет важную роль. Она помогает определить положение объекта на плоскости и правильно его изобразить. Для этого необходимо знать координаты точек объекта в трехмерной системе координат и применить операции проектирования.
Операции проектирования основываются на принципе подобия треугольников и позволяют найти соответствие между точками трехмерного пространства и точками плоскости проекции. Благодаря этому, при проецировании прямой из трехмерного пространства на плоскость, сохраняется ее направление и длина, а также углы между прямой и другими объектами.
Таким образом, система координат является основой для прямой проекции и необходима для правильного изображения объектов на плоскости с сохранением их пропорций.
Основные принципы построения прямой проекции в натуральную величину

При построении прямой проекции в натуральную величину необходимо учесть несколько основных принципов:
| 1. | Выбор масштаба. Масштаб выбирается исходя из необходимости показать объект с наиболее выразительной точностью без потери данных. Оптимальный масштаб обеспечивает наглядность и удобство восприятия. |
| 2. | Перенос точек. Для построения прямой проекции необходимо определить координаты точек объекта на плоскости. При этом следует учесть геометрическую связь между точками и сохранить их пространственные отношения. |
| 3. | Учет перспективы. При построении прямой проекции следует учитывать перспективу – изменение размеров и форм объекта в зависимости от его удаленности от наблюдателя. Это позволяет создать иллюзию глубины и объемности. |
| 4. | Закономерности светотени. Проекция в натуральную величину также должна учитывать освещение объекта и правила формирования светотеней. Это помогает создать реалистичность и объемность изображения. |
Соблюдение этих основных принципов позволяет создать точное и наглядное изображение объекта в натуральную величину. Прямая проекция является важным инструментом для анализа и проектирования объектов и помогает представить их в реальном масштабе.
Инструменты и способы прямой проекции для точных измерений

Для точных измерений и проекций прямых, используется ряд специальных инструментов и методов. В данном разделе мы рассмотрим некоторые из них.
1. Линейка
Простой и наиболее распространенный инструмент для прямой проекции - линейка. Линейка позволяет измерять расстояние между двумя точками на плоскости и строить прямые линии. Она может быть изготовлена из металла, пластика или дерева и иметь различную длину.
2. Транспортир
Транспортир - это инструмент, который используется для измерения углов и в процессе прямой проекции. Он состоит из полукруглой шкалы, на которой указаны углы от 0 до 180 градусов. Транспортир помогает определить углы между прямыми и находить точки на прямой проекции.
3. Угольник
Угольник - это инструмент, позволяющий измерять и строить прямые углы. Он состоит из двух перпендикулярных линеек, связанных под углом 90 градусов. При использовании угольника можно создавать прямоугольники и другие формы, а также проверять прямые углы и перпендикулярность.
4. Компас
Компас - это инструмент, используемый для построения окружностей и дуг. Он состоит из острия и линейки с делениями. Компас позволяет производить прямую проекцию окружностей и устанавливать точки на них.
5. Геодезический инструментарий
Для более точных измерений и проекций, в геодезии используется специальный геодезический инструментарий. Он включает в себя теодолиты, нивелиры и другие приборы, которые позволяют производить прецизионные измерения и строить точные прямые проекции с высокой точностью.
В зависимости от требуемой точности измерений и проекций, выбираются соответствующие инструменты и методы. Важно помнить, что правильное использование инструментов и методов прямой проекции является ключевым фактором для достижения точных результатов.
Практическое применение прямой проекции в различных областях

В архитектуре прямая проекция используется для создания планов зданий, фасадов и интерьеров. Она позволяет точно передать размеры, пропорции и расположение объектов, что особенно важно при проектировании и строительстве.
В инженерии прямая проекция помогает в создании технических чертежей и схем. Она позволяет передавать информацию о размерах, форме и расположении деталей, что важно для изготовления и сборки механизмов и конструкций.
В графическом дизайне прямая проекция позволяет создавать плакаты, рекламные листовки и другие материалы. Она позволяет передавать информацию о различных предметах и идеях в понятной и эффективной форме.
Прямая проекция также находит применение в искусстве, особенно в живописи и графике. Она позволяет передать пространственные отношения и глубину объектов, создавая натуральное и реалистичное изображение.
В образовании и научных исследованиях прямая проекция используется для визуализации и анализа различных данных. Она позволяет создавать эффективные и понятные презентации, графики и диаграммы.
В целом, прямая проекция является мощным инструментом, который находит широкое применение в различных областях. Она помогает передавать информацию о размерах, форме и пространственных отношениях объектов, делая их понятными и доступными для восприятия.
Преимущества и ограничения прямой проекции

- Преимущества прямой проекции:
1. Простота: Прямая проекция является простым и понятным методом отображения трехмерных объектов. Она позволяет легко представить объекты в двумерном пространстве.
2. Сохранение пропорций: В прямой проекции пропорции объекта сохраняются, что позволяет точно представить его размеры и форму.
3. Удобство измерения: Благодаря прямой проекции, можно легко измерить расстояния и углы на плоскости, что делает ее полезной для инженерных и строительных задач.
- Ограничения прямой проекции:
1. Потеря глубины: В прямой проекции не передается глубина объекта, что может быть недостатком при представлении сложных трехмерных форм.
2. Искажение формы: При прямой проекции объекты, находящиеся дальше от плоскости проекции, могут быть искажены. Это ограничение может быть преодолено путем использования других методов проекции, таких как перспективная проекция.
3. Ограничение на число измерений: Прямая проекция позволяет представить объекты только в двумерном пространстве. Для представления более сложных трехмерных объектов требуется использование других методов проекции.
Таким образом, прямая проекция является полезным методом для представления трехмерных объектов в двухмерном пространстве, но она имеет свои ограничения. В зависимости от конкретной задачи и требований, может потребоваться использование других методов проекции для более точного и полного представления объектов.



