Движение тела по окружности - одно из фундаментальных понятий физики и математики. В этой статье мы рассмотрим особенности такого движения, изучим основные законы и приведем примеры из реальной жизни, где тело движется равномерно по окружности.
Когда тело движется по окружности, его скорость постоянна, но направление движения постоянно меняется. Такое движение может быть наблюдаемо на плоскости или в трехмерном пространстве. Например, вращение ручки светильника или движение планеты вокруг Солнца являются примерами такого движения.
Важно отметить, что для тела, движущегося равномерно по окружности, существуют определенные законы. Например, радиус окружности, по которой движется тело, определяет его перемещение за определенный период времени. Кроме того, с помощью угловой скорости и центростремительного ускорения можно вычислить значения этих величин и предсказать движение тела.
Основные особенности движения тела по окружности
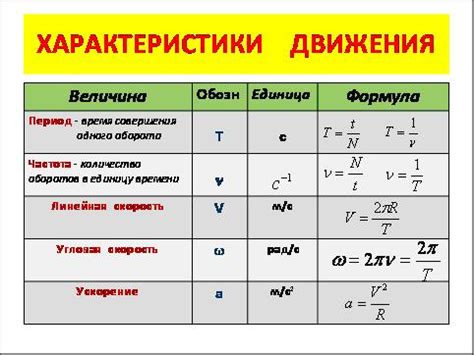
Движение тела по окружности имеет ряд особенностей, которые важны для понимания его характеристик и свойств. Вот некоторые из них:
| 1. | Траектория движения | Тело движется по окружности с постоянной радиусом. Траектория тела представляет собой замкнутую кривую, а каждая точка траектории обладает постоянным расстоянием от центра окружности. |
| 2. | Угловая скорость | Движение тела по окружности характеризуется угловой скоростью, которая является постоянной величиной. Угловая скорость определяет, сколько градусов (или радиан) тело проходит за единицу времени. |
| 3. | Период движения | Период движения тела по окружности - это время, за которое тело совершает полный оборот вокруг центра окружности. Он обратно пропорционален угловой скорости и определяется формулой T = 2π/ω, где T - период, а ω - угловая скорость. |
| 4. | Линейная скорость | Линейная скорость тела, движущегося по окружности, зависит от его радиуса и угловой скорости. Линейная скорость равна произведению радиуса окружности на угловую скорость. |
| 5. | Центростремительное ускорение | При движении тела по окружности возникает центростремительное ускорение, которое направлено к центру окружности. Величина центростремительного ускорения определяется формулой ac = v^2 / r, где ac - центростремительное ускорение, v - линейная скорость, r - радиус окружности. |
Эти особенности движения тела по окружности помогают описать его кинематические характеристики и определить различные законы, которые применяются при решении задач с движением по окружности.
Угловая скорость и линейная скорость

Когда тело движется по окружности, его движение описывается не только линейной скоростью, но и угловой скоростью.
Угловая скорость – это величина, которая определяет, как быстро тело поворачивается вокруг оси. Она измеряется в радианах в секунду и обозначается символом ω. Угловая скорость рассчитывается как отношение угла поворота к времени, необходимому для его выполнения. Таким образом, угловая скорость равна изменению угла на единицу времени.
Линейная скорость представляет собой величину, которая характеризует скорость перемещения тела по окружности. Она измеряется в метрах в секунду и обозначается символом v. Линейная скорость рассчитывается как произведение радиуса окружности на угловую скорость.
Связь между угловой скоростью и линейной скоростью можно выразить следующей формулой:
| Угловая скорость | ω |
|---|---|
| Линейная скорость | v |
| Радиус окружности | r |
Таким образом, линейная скорость всегда равна произведению радиуса окружности на угловую скорость:
v = r * ω
Это означает, что при увеличении угловой скорости, линейная скорость также увеличивается. Также стоит отметить, что линейная скорость всегда тангенциальна к направлению движения и изменяется вместе с ним.
Центростремительное ускорение
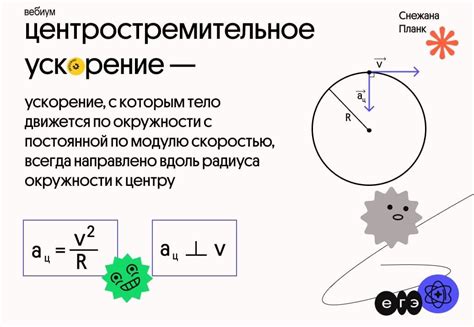
Если тело движется по окружности с постоянной скоростью, то его скорость постоянна, однако направление скорости постоянно меняется. Именно это изменение направления скорости и вызывает центростремительное ускорение.
Центростремительное ускорение определяется формулой:
aцс = v2/R
где aцс - центростремительное ускорение, v - скорость тела, R - радиус окружности.
Центростремительное ускорение является инерционным ускорением и всегда направлено к центру окружности. Оно обуславливает изменение направления скорости тела и является причиной изменения направления движения.
Примером явления центростремительного ускорения может служить движение автомобиля по круговому повороту. Когда автомобиль поворачивает, его скорость и направление движения изменяются под действием центростремительного ускорения.
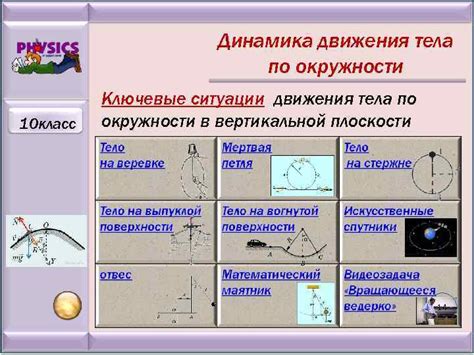
Законы Ньютона и движение по окружности

При движении тела по окружности, действуют законы, которые были сформулированы Исааком Ньютоном. Эти законы определяют движение объекта и позволяют понять его свойства и особенности.
Первый закон Ньютона, также известный как закон инерции, гласит, что тело будет продолжать двигаться равномерно и прямолинейно, пока на него не будет действовать внешняя сила. В контексте движения по окружности это означает, что даже если тело имеет постоянную скорость, оно будет отклоняться от прямолинейного движения и двигаться по окружности только при действии силы, направленной к центру окружности.
Второй закон Ньютона гласит, что силы, действующие на тело, равны произведению его массы на ускорение. Для тела, движущегося по окружности, ускорение является радиальным, направленным к центру окружности. Это означает, что на тело, движущееся по окружности, действует радиальная сила с постоянным модулем, необходимая для поддержания постоянного радиуса окружности.
Третий закон Ньютона, также известный как закон действия и противодействия, гласит, что на каждое действие действует равное и противоположное по направлению действие. В контексте движения по окружности это означает, что если тело действует на центростремительную силу, то центростремительная сила действует на тело в противоположном направлении.
Таким образом, законы Ньютона объясняют движение тела по окружности и позволяют анализировать его свойства и особенности. Они позволяют понять, почему тело не движется по прямой линии, а движется по окружности, а также какие силы действуют на это тело.
Примеры движения тела по окружности

| Пример | Описание |
|---|---|
| Движение спутника | Спутники движутся по окружности вокруг планеты или другого небесного тела. Это движение основано на балансе между гравитацией, служащей центростремительной силой, и прямолинейной инерцией тела. |
| Вращение колеса | Когда автомобиль движется по дороге, колеса выполняют движение по окружности. Такое движение позволяет автомобилю ехать прямо и поворачивать. |
| Колебание маятника | Маятник, двигающийся в плоскости, описывает гармоническое колебание. Если маятник немного сместить в сторону, он начнет двигаться по окружности. Колебание маятника по окружности называется круговым колебанием. |
| Движение электрона в атоме | Электроны, обращаясь вокруг ядра атома, движутся по эллиптическим или круговым орбитам. Это движение определяет электронную структуру атома и его свойства. |
Практическое применение движения по окружности
Движение по окружности имеет множество практических применений в различных областях.
В астрономии движение планет вокруг Солнца и Луны вокруг Земли являются примерами движения по окружности. Это явление позволяет исследовать вращение и орбиты небесных тел, прогнозировать их положение и движение.
В авиации движение по окружности используется в маневрах самолетов, таких как круговые обходы и заходы на посадку. Пилоты используют принципы движения по окружности для управления и изменения высоты и направления полета.
В физике движение по окружности отыгрывает важную роль при изучении вращательного движения. Множество экспериментов проводятся с помощью центробежных сил, создаваемых при движении по окружности.
В машиностроении движение по окружности используется в роторах и валах для создания движения и передачи энергии. Множество механизмов, таких как шкивы и зубчатые колеса, основаны на принципе движения по окружности.
Движение по окружности также находит применение в спорте. Например, в гимнастике и фигурном катании спортсмены выполняют различные трюки, используя принципы движения по окружности.
В искусстве движение по окружности может быть использовано для создания эстетически приятных композиций и узоров. Это применяется в различных видах искусства, таких как живопись, фотография и графический дизайн.
Таким образом, движение по окружности является важным физическим явлением, которое находит применение во множестве областей человеческой деятельности.



