Изучение площади треугольника – одно из ключевых понятий геометрии, которое рассматривается в школе. Этот урок позволяет учащимся понять, как найти площадь треугольника, используя различные методы и формулы. Знание площади треугольника является необходимым навыком для решения задач, связанных с измерением площадей геометрических фигур.
Изучение площади треугольника начинается с основных понятий геометрии и формул, которые позволяют вычислить площадь треугольника. Ученики узнают, что площадь треугольника можно найти, умножив половину его высоты на основание. Рассматриваются различные способы измерения высоты и основания треугольника, а также особенности треугольников разных типов – равносторонних, равнобедренных и разносторонних.
Изучение площади треугольника – это не просто вычисление числа, это развитие способности абстрагироваться от конкретных задач, анализировать и решать геометрические задачи с помощью логического мышления. Урок обучает учеников логическим законам геометрии, которые также пригодятся им в решении задач не только на площадь треугольника, но и на площадь других геометрических фигур.
Что такое площадь треугольника?

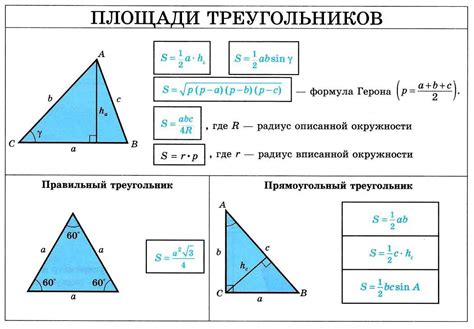
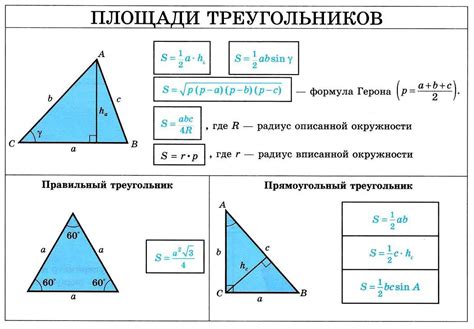
Для того чтобы вычислить площадь треугольника, мы используем формулу, основанную на его основании и высоте. Основание – это одна из сторон треугольника, а высота – перпендикуляр, опущенный из вершины к основанию. Формула для нахождения площади треугольника:
S = (1/2) * a * h
Где S – площадь треугольника, a – длина основания, h – длина высоты.
Важно помнить, что основание и высота треугольника должны быть измерены в одних и тех же единицах измерения. Для нахождения площади треугольника также можно использовать другие формулы, если известны длины его сторон или координаты его вершин.
Подсчет площади треугольника при изучении геометрии в школе полезен тем, что помогает развивать навыки аналитического мышления, работу с числами и понимание различных свойств геометрических фигур. Кроме того, понимание площади треугольника может быть полезным в реальной жизни, например, при решении задач по строительству, архитектуре или дизайну.
Итак, площадь треугольника – это важное понятие в геометрии, которое помогает измерить поверхность этой фигуры и применяется в различных сферах жизни.
Значение и определение

Площадь треугольника может быть вычислена по различным формулам, в зависимости от доступных данных о треугольнике. Одна из самых распространенных формул - это формула Герона, которая позволяет вычислить площадь треугольника, если известны длины его сторон.
Важно отметить, что площадь треугольника всегда будет положительным числом, так как площадь является мерой положительной величины двумерной площади. Если треугольник имеет нулевую площадь, это означает, что он вырожденный и представляет собой множество из трех коллинеарных точек.
Площадь треугольника имеет ряд важных свойств, таких как аддитивность (площадь объединения двух треугольников равна сумме их площадей) и монотонность (если треугольник A содержится в треугольнике B, то площадь треугольника A меньше площади треугольника B).
Изучение площади треугольника в школьной программе помогает развить логическое и пространственное мышление, а также приобрести навыки работы с формулами и вычислениями.
Взаимосвязь с другими фигурами
Например, площадь треугольника может быть использована для определения площади других фигур. Если знать высоту треугольника и его основание, то площадь можно вычислить по формуле S = 0,5 * h * a, где S - площадь, h - высота, а - основание.
Кроме того, треугольник имеет много общего с другими фигурами. Например, разделение треугольника на две равные части, используя медиану, дает два равных треугольника. Также, треугольник может быть преобразован в прямоугольник, если соединить его другой точкой на противоположной стороне.
Изучение взаимосвязи треугольников с другими фигурами помогает развивать логическое мышление, умение анализировать и применять геометрические преобразования. Понимание этой взаимосвязи позволяет увидеть геометрическую гармонию и упрощает решение задач из разных областей науки и техники.
Как изучают площадь треугольника в школе
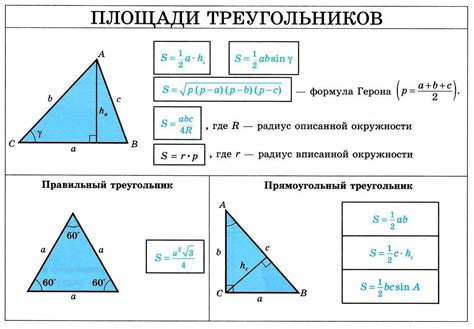
В учебном процессе школьники узнают несколько способов вычисления площади треугольника. Одним из самых распространенных способов является использование формулы площади треугольника, основанной на основании и высоте треугольника. Данная формула выглядит следующим образом:
S = 0.5 * a * h
где S - площадь треугольника, a - длина основания треугольника, h - высота треугольника, опущенная на это основание.
Школьники также изучают другие методы вычисления площади треугольника, такие как использование полупериметра и радиуса описанной окружности.
Знание площади треугольника позволяет школьникам не только решать упражнения и задачи, связанные с треугольниками, но и применять эти навыки в реальных ситуациях. Например, они могут использовать понятие площади треугольника для определения площади поля, постройки или другого объекта.
Таким образом, изучение площади треугольника в школе является важным и полезным элементом образования, который развивает навыки аналитического мышления, геометрического рассуждения и применения математических концепций в реальной жизни.
Объяснение на примере задач

Пример 1:
Предположим, у нас есть треугольник с основанием 4 см и высотой 3 см. Нам нужно найти его площадь.
Первым шагом мы используем формулу для нахождения площади треугольника: площадь = (основание * высота) / 2.
Вставив значения из задачи в формулу, мы получим площадь = (4 * 3) / 2 = 12 / 2 = 6 см².
Таким образом, площадь треугольника равна 6 см².
Пример 2:
Пусть у нас есть треугольник с сторонами длиной 5 см, 12 см и 13 см. Мы хотим найти его площадь.
Для решения этой задачи мы можем использовать формулу Герона, которая связана со сторонами треугольника: площадь = √(p * (p - a) * (p - b) * (p - c)), где a, b и c - длины сторон треугольника, а p - полупериметр (p = (a + b + c) / 2).
Сначала вычислим полупериметр: p = (5 + 12 + 13) / 2 = 30 / 2 = 15.
Затем вставим значения в формулу: площадь = √(15 * (15 - 5) * (15 - 12) * (15 - 13)) = √(15 * 10 * 3 * 2) = √(900) = 30 см².
Таким образом, площадь треугольника равна 30 см².
Видеоуроки по площади треугольника
Видеоуроки по площади треугольника доступны на различных платформах и видеохостингах, таких как YouTube, Coursera, Khan Academy и многих других. Эти уроки представляют собой наглядное объяснение основных принципов расчета площади треугольника и различных способов его измерения.
Популярные видеоуроки по площади треугольника включают в себя ряд примеров и задач, решение которых поможет учащимся лучше разобраться с этой концепцией. Также обычно в этих уроках приводятся основные формулы для вычисления площади треугольника по разным заданным параметрам, например, по длинам сторон или по высоте треугольника.
Видеоуроки по площади треугольника являются отличным инструментом для расширения понимания материала и подготовки к тестам и экзаменам. Они предлагают возможность повторить и закрепить изученную информацию и предлагают интересный и эффективный способ изучения данной темы.
Ознакомление с видеоуроками по площади треугольника поможет школьникам улучшить свои математические навыки, усовершенствовать понимание геометрии и применять полученные знания на практике.
Почему изучение площади треугольника важно
Изучение площади треугольника имеет важное значение в школе, так как позволяет развить ученикам навыки анализа, логики и решения математических задач. Знание понятия площади треугольника необходимо для понимания и решения более сложных задач и практических проблем.
Изучение площади треугольника помогает ученикам улучшить свои навыки построения геометрических фигур и работу с формулами. Он также развивает важные качества, такие как абстрактное мышление, творческое решение проблем и систематический подход к учебе.
Понимание площади треугольника полезно не только в учебе, но и в повседневной жизни. Зная как найти площадь треугольника, мы можем применить этот навык для решения практических задач, таких как измерение площади участка земли или рассчет площади фасада здания.
Поэтому, изучение площади треугольника является важным этапом математического образования, который помогает ученикам развить навыки и знания, необходимые для успешного и продуктивного будущего.



