Математика всегда ассоциируется с числами, формулами и арифметическими операциями. Однако, иногда она может представлять собой настоящую загадку. Одной из таких загадок является корень в квадрат – операция, которая, на первый взгляд, может показаться противоречивой. Что же такое корень в квадрат, и какие условия и правила нужно соблюдать при его возведении?
Корень в квадрат (√x²) – это операция, обратная возведению в квадрат. Если при возведении числа в квадрат мы умножаем его само на себя, то для корня в квадрат мы ищем число, которое при возведении в квадрат даст исходное число. Поэтому корень в квадрат является противоположностью возведению в квадрат и позволяет нам найти исходное число из его квадрата.
Однако, важно помнить, что корень в квадрат из отрицательного числа не существует в области действительных чисел. Дело в том, что при возведении любого числа в квадрат результат всегда будет неотрицательным числом. Поэтому, чтобы извлечь корень в квадрат из отрицательного числа, мы должны перейти к комплексным числам, где у нас есть мнимая единица (i), представляющая корень из -1.
Условия возведения корня числа в квадрат
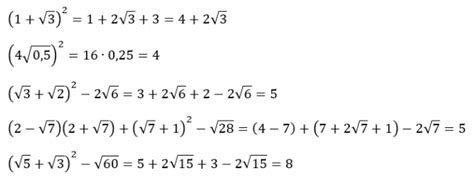
Условия возведения корня числа в квадрат:
1. Действительные числа. Возведение корня числа в квадрат применяется только к действительным числам. Комплексные числа не могут быть возведены в квадрат, так как они имеют мнимую часть.
2. Положительное число. Число, которое будет возводиться в квадрат, должно быть положительным. Возведение отрицательного числа в квадрат приведет к получению положительного числа, но перевернет его знак.
3. Число без остатка. Если число имеет дробную часть, оно должно быть округлено до целого числа перед возведением в квадрат.
Пример:
Возведение корня числа 4 в квадрат:
42 = 4 * 4 = 16
Возведение корня числа 5.5 в квадрат:
5.52 = 5.5 * 5.5 = 30.25
Возведение корня числа -3 в квадрат:
(-3)2 = (-3) * (-3) = 9
Результатом возведения корня числа в квадрат будет всегда положительное число.
Основные правила

При возведении корня в квадрат необходимо учитывать следующие правила:
- Корень в квадрат из положительного числа всегда будет положительным числом.
- Корень в квадрат из нуля равен нулю, так как любое число возводится в квадрат будет давать ноль.
- Корень в квадрат из отрицательного числа не существует в области действительных чисел, так как квадратные корни только избирательно извлекаются из положительных чисел.
- При суммировании корней в квадрате следует использовать свойства сложения, сначала складывая числа под корнем, а затем извлекая корень.
- При умножении или делении корней в квадрате использование свойств умножения или деления позволяет упростить задачу, применяя операции с числами под корнем.
Знание и применение этих правил позволят правильно и эффективно производить операции с корнем в квадрате и получать верные результаты.
Исключения и специальные случаи

При возведении корня в квадрат есть несколько исключений и особых случаев, которые важно учесть. Вот некоторые из них:
1. Негативное число: Корень квадратный из отрицательного числа равен комплексному числу. Комплексное число имеет вещественную и мнимую части. Для обозначения мнимой части используется символ i. Например, корень квадратный из -9 равен 3i.
2. Ноль: Корень квадратный из нуля равен нулю, так как 0 умноженное на себя равно 0.
3. Дробное число: Корень квадратный из дробного числа можно вычислить, но результат тоже будет дробным числом. Например, корень квадратный из 0.25 равен 0.5.
4. Корень из корня: Корень квадратный (или другой четный корень) из корня нельзя вычислить таким же образом, как и обычный корень. В этом случае необходимо использовать свойства корней для упрощения выражения.
Эти исключения и специальные случаи помогают понять, что возведение корня в квадрат не всегда приводит к однозначному результату, и требуется учитывать контекст и условия задачи.



