Квадрат и прямоугольник – два понятия, которые часто встречаются в геометрии. Но существует ли прямая связь между ними? Эта статья расскажет о том, можно ли считать любой квадрат прямоугольником, а также разъяснит, в чем заключается их основное отличие.
Однако это утверждение не совсем точное. Хоть квадрат и является прямоугольником, не каждый прямоугольник может быть квадратом. Это объясняется тем, что квадрат является частным случаем прямоугольника с определенными характеристиками. Для того чтобы прямоугольник стал квадратом, необходимо, чтобы все его стороны были равны друг другу, тогда можно сказать, что данный прямоугольник становится квадратом.
Квадрат и прямоугольник: теоретические сходства и различия

Основное сходство между квадратом и прямоугольником заключается в том, что оба они являются параллелограммами, то есть фигурами с противоположными сторонами, которые параллельны и имеют одинаковые длины. Также и квадрат, и прямоугольник являются многоугольниками, у которых все углы равны 90 градусов.
Однако, основное отличие между квадратом и прямоугольником состоит в том, что все стороны квадрата имеют одинаковую длину. Это означает, что каждый квадрат является прямоугольником, но не каждый прямоугольник является квадратом. Прямоугольник может иметь разные длины сторон, в то время как квадрат имеет равные стороны.
Другое отличие между квадратом и прямоугольником заключается в их свойствах. Например, квадрат является специальным случаем прямоугольника, все его диагонали равны, и он имеет больше симметрий, чем прямоугольник.
Итак, хотя все квадраты являются прямоугольниками, не все прямоугольники являются квадратами. Квадрат и прямоугольник имеют сходства, но их отличия очевидны. Это важно учитывать при работе с геометрическими фигурами и формулами, чтобы избежать путаницы и ошибок.
| Характеристика | Квадрат | Прямоугольник |
|---|---|---|
| Все стороны равны | Да | Нет |
| Углы | Все равны 90 градусов | Все равны 90 градусов |
| Диагонали | Все равны | Могут быть разной длины |
| Симметрии | Больше | Меньше |
Строение и геометрические характеристики квадрата

Каждая сторона квадрата равна другой, и он может быть описан с помощью параметра a, обозначающего длину одной его стороны.
У квадрата есть несколько геометрических характеристик. Периметр квадрата равен сумме длин всех его сторон и вычисляется по формуле P = 4a. Площадь квадрата равна квадрату длины его стороны и вычисляется по формуле S = a^2.
Квадрат обладает не только равными сторонами, но и равными диагоналями. Диагональ квадрата является линией, соединяющей противоположные вершины. Длина диагонали квадрата вычисляется с помощью теоремы Пифагора: D = √(a^2 + a^2) = √2a.
Симметрия является также одной из важных характеристик квадрата. Все оси симметрии квадрата проходят через его центр и делят его на две половины, которые симметричны относительно каждой оси.
Особенности прямоугольника по сравнению с квадратом
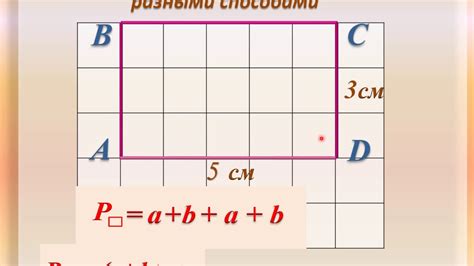
Основная особенность прямоугольника заключается в том, что у него параллельные стороны, которые могут иметь различные длины. Это отличает прямоугольник от квадрата, у которого все стороны равны. У прямоугольника соседние стороны могут быть разной длины, но они всегда будут параллельными.
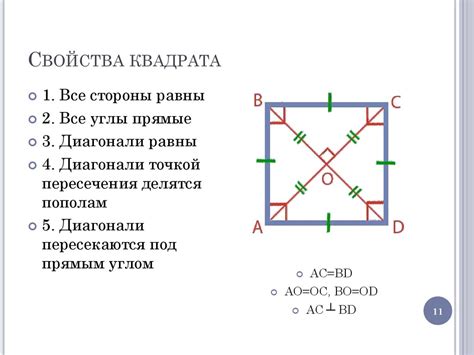
Еще одна отличительная черта прямоугольника - его диагонали. Диагонали прямоугольника всегда равны между собой и делят фигуру на два равных треугольника. В случае квадрата, его диагонали также равны, и каждая из них является осью симметрии фигуры.
Прямоугольники широко используются в геометрии и в повседневной жизни. Они являются основой для построения различных фигур и конструкций. Прямоугольник можно рассматривать как более общий случай квадрата, так как любой квадрат является прямоугольником с равными сторонами.
| Прямоугольник | Квадрат |
|---|---|
| Разные длины сторон | Все стороны равны |
| Параллельные стороны | Параллельные стороны |
| Диагонали равны | Диагонали равны и являются осями симметрии |
Определение квадрата и прямоугольника в геометрической терминологии
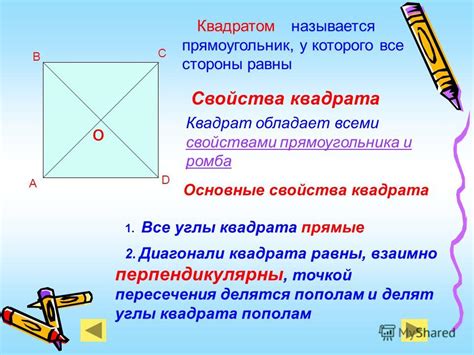
Квадрат - это особый вид прямоугольника, у которого все стороны равны друг другу и все углы прямые. Таким образом, все стороны квадрата являются равными прямолинейными отрезками, а каждый его угол равен 90 градусам.
Прямоугольник - это четырехугольник, у которого противоположные стороны параллельны и равны друг другу. Другими словами, в прямоугольнике все углы прямые, но стороны не обязательно равны друг другу. Единственным обязательным свойством прямоугольника является равенство противоположных сторон и прямолинейность углов.
Таким образом, квадрат является особым видом прямоугольника, у которого все стороны равны. В то же время не все прямоугольники являются квадратами, так как они могут иметь разные стороны, но все равно быть прямоугольными.
Важно отметить, что прямоугольник с достаточно большой разницей между сторонами может называться "продолговатым прямоугольником", но это уже более специфическое определение, а не базовое свойство прямоугольника.
Сочетание сторон и углов в квадрате и прямоугольнике

Более подробно рассмотрим особенности этих фигур:
- Квадрат - это частный случай прямоугольника, у которого все стороны равны. Все углы квадрата также равны 90 градусов.
- Прямоугольник - это четырехугольник, у которого противоположные стороны равны по длине и все углы равны 90 градусов.
Таким образом, можно сказать, что всякий квадрат является прямоугольником, но не каждый прямоугольник является квадратом.
Прямоугольник может иметь разные длины сторон, в то время как у квадрата все стороны одинаковые.
Сочетания сторон и углов в квадрате и прямоугольнике определяют их свойства и применения в геометрии и на практике. Оба этих вида
четырехугольников широко используются: прямоугольники в строительстве, дизайне, изготовлении мебели, а квадраты - в узкоспециализированных
задачах и исследованиях.
Условия, необходимые для различения квадрата от прямоугольника
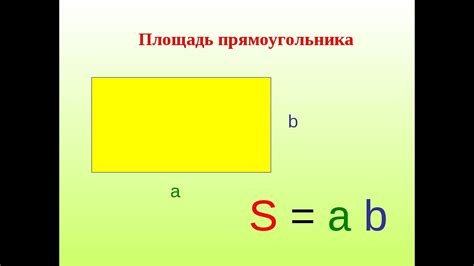
Основное отличие между квадратом и прямоугольником заключается в соотношении его сторон. Для квадрата все стороны имеют одинаковую длину, в то время как у прямоугольника длина двух противоположных сторон может быть разной.
Используя таблицу, можно более наглядно представить основные условия, необходимые для различения квадрата от прямоугольника:
| Квадрат | Прямоугольник |
|---|---|
| Все стороны равны | Длина противоположных сторон различна |
| Углы между сторонами всегда 90 градусов | Углы между сторонами всегда 90 градусов |
Таким образом, если все стороны фигуры равны и углы между сторонами равны 90 градусам, то это квадрат. Если же длина двух противоположных сторон отличается, то это прямоугольник.
Возможность превращения квадрата в прямоугольник
Возможно ли превратить квадрат в прямоугольник? Технически да, это возможно. Для этого нужно изменить длину или ширину квадрата так, чтобы они были разными. Размещая четыре одинаковых квадрата на плоскости один за другим или друг рядом, вы можете образовать прямоугольник. Это демонстрирует, что квадрат является одной из разновидностей прямоугольников.
Примером превращения квадрата в прямоугольник может служить игральная кость. Куб состоит из шести квадратных граней, каждая из которых является квадратом. Однако, когда вы бросаете куб и он останавливается на одной из граней, плоскость, образуемая этой гранью, становится прямоугольной. Таким образом, квадраты, составляющие грани куба, могут быть превращены в прямоугольники.
Возможность превращения прямоугольника в квадрат
Для превращения прямоугольника в квадрат необходимо, чтобы все его стороны были равны. Если стороны прямоугольника имеют равные значения, то он автоматически становится квадратом. В этом случае можно сказать, что каждый квадрат является прямоугольником, но не каждый прямоугольник является квадратом.
В противном случае, если хотя бы одна из сторон прямоугольника отличается по длине от других, он не может быть назван квадратом.
Превращение прямоугольника в квадрат может быть достигнуто путем изменения длин сторон. Например, если одну из сторон укоротить или удлинить так, чтобы она стала равной другой стороне прямоугольника, то фигура становится квадратом.



