Прямоугольник и параллелограмм - две фигуры с геометрическими свойствами, которые мы часто встречаем в нашей повседневной жизни. Возможно, кажется, что все прямоугольники тоже являются параллелограммами, ведь у них такое же свойство - противоположные стороны попарно параллельны. Однако, это заблуждение.
Прямоугольник - это параллелограмм с дополнительным свойством: углы прямоугольника равны 90 градусам. То есть прямоугольник - это параллелограмм, у которого все углы являются прямыми. Таким образом, можно сказать, что каждый прямоугольник - это особый вид параллелограмма, обладающий дополнительными ограничениями по углам.
В отличие от прямоугольника, у параллелограмма углы могут быть различными. Главное условие для параллелограмма - это параллельность противоположных сторон. Это означает, что две противоположные стороны параллелограмма всегда попарно параллельны. Остальные свойства параллелограмма могут меняться: углы могут быть острыми, тупыми или прямыми, а стороны могут быть равными или неравными.
Прямоугольник и параллелограмм: особенности и сходства

Особенности прямоугольника:
1. Прямоугольник - это четырехугольник, у которого все углы прямые (равны 90 градусам).
2. Противоположные стороны прямоугольника равны друг другу по длине.
3. Диагонали прямоугольника также равны, и их точка пересечения делит каждую диагональ пополам.
4. Площадь прямоугольника вычисляется по формуле: S = a * b, где a и b - длины его сторон.
Особенности параллелограмма:
1. Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны.
2. Противоположные углы параллелограмма также равны.
3. Диагонали параллелограмма делятся точкой пересечения пополам.
4. Площадь параллелограмма вычисляется как произведение длины одной его стороны на высоту, опущенную на эту сторону.
Общие сходства прямоугольника и параллелограмма:
1. Они оба являются четырехугольниками.
2. У них могут быть равные стороны и равные углы.
3. Диагонали обеих фигур обладают свойством делиться пополам.
Таким образом, хотя прямоугольник и параллелограмм имеют свои особенности, они также обладают несколькими общими свойствами.
Прямоугольник - это особый вид параллелограмма
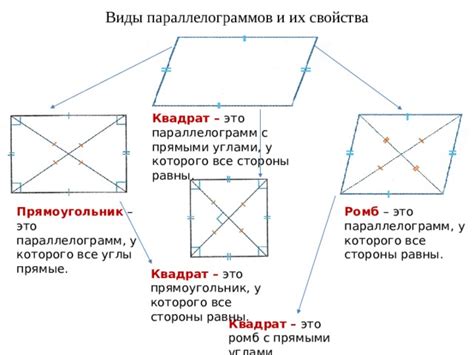
Основная особенность прямоугольника заключается в том, что все его углы равны 90 градусам. Это позволяет нам использовать его в различных областях: от геометрии до архитектуры.
Параллельные стороны прямоугольника также являются равными, что делает его особенно удобным для вычислений и измерений. Благодаря этому свойству прямоугольник активно применяется в строительстве и дизайне интерьеров.
Кроме того, прямоугольник имеет две оси симметрии: горизонтальную и вертикальную. Это позволяет нам делать отражения и повороты фигуры без изменения ее формы и размеров.
Таким образом, прямоугольник является важной геометрической фигурой, которая обладает специфическими свойствами. Благодаря своей простоте и функциональности он находит широкое применение в различных сферах нашей жизни.
Характеристики, определяющие прямоугольник

- Все углы прямые: У прямоугольника все углы равны 90 градусам. Это отличает его от других параллелограммов, у которых могут быть наклонные углы.
- Противоположные стороны равны: В прямоугольнике противоположные стороны параллельны и равны друг другу. Это свойство помогает определить прямоугольник, даже если его углы неизвестны или трудно измерить.
- Диагонали пересекаются в серединах: Диагонали прямоугольника делятся пополам в точках пересечения. Если провести диагонали в прямоугольнике и они не пересекутся в серединах, это будет признаком, что фигура не является прямоугольником.
- Равенство противоположных углов: У прямоугольника противоположные углы равны друг другу. Если углы не равны, это значит, что фигура не является прямоугольником.
- Сумма углов в прямоугольнике равна 360 градусам: Так как у прямоугольника все углы прямые, сумма всех его углов будет равна 360 градусам. Если сумма углов не равна 360 градусам, это будет признаком, что фигура не является прямоугольником.
С учетом этих характеристик можно легко определить, является ли фигура прямоугольником или нет. Это знание полезно при решении геометрических задач и в повседневной жизни, например при измерении и разметке объектов.
Особенности параллелограмма от прямоугольника

Основные особенности параллелограмма от прямоугольника:
- Углы параллелограмма могут быть любыми и не обязательно прямыми, в то время как углы прямоугольника всегда являются прямыми.
- Стороны параллелограмма могут быть любых длин и не обязательно равны, тогда как в прямоугольнике все стороны равны.
- В параллелограмме диагонали могут иметь любую длину и не обязательно быть равными, в то время как в прямоугольнике диагонали равны и делятся пополам.
Эти особенности делают параллелограмм универсальной геометрической фигурой, позволяющей строить разнообразные формы, включая прямоугольник. Прямоугольник, в свою очередь, является особым случаем параллелограмма, где все углы прямые и все стороны равны, что обеспечивает его симметричность и простоту в решении геометрических задач.



