Существует множество различных методов определения, является ли треугольник прямоугольным. В данной статье мы рассмотрим несколько способов, которые помогут вам определить, можно ли назвать данный треугольник прямоугольным.
Прежде всего, необходимо знать, что прямоугольным называется треугольник, у которого один из углов равен 90 градусам. Мы можем воспользоваться этим свойством для определения, является ли треугольник прямоугольным.
Условия существования

Прямоугольный треугольник обладает определенными условиями существования, которые необходимо учитывать при его определении.
Первое условие – сумма квадратов катетов (двух меньших сторон) должна быть равна квадрату гипотенузы (наибольшей стороны). То есть, если стороны треугольника обозначены как a, b и c, где c – гипотенуза, то должно выполняться равенство a^2 + b^2 = c^2.
Второе условие – все стороны треугольника должны быть положительными числами.
Третье условие – сумма длин любых двух сторон треугольника должна быть больше длины третьей стороны. Иначе треугольник не существует.
Если все эти условия выполняются, то треугольник является прямоугольным.
Взаимосвязь сторон треугольника
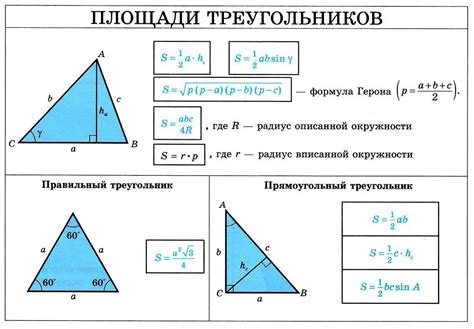
В прямоугольном треугольнике стороны принято называть катетами и гипотенузой. Катеты - это две стороны, которые образуют прямой угол, а гипотенуза - это самая длинная сторона треугольника, которая противоположна прямому углу.
Существует следующая взаимосвязь между сторонами прямоугольного треугольника:
- Квадрат гипотенузы равен сумме квадратов катетов. Это выражается формулой: c2 = a2 + b2
- Каждый катет является половиной гипотенузы, если сравнивать их проекции на гипотенузу.
- Катеты в прямоугольном треугольнике являются противоположными катетами, то есть длины катетов обратно пропорциональны.
- Катеты в прямоугольном треугольнике пропорциональны соответствующим прилежащим отрезкам гипотенузы, когда делятся ею.
Зная длины двух сторон прямоугольного треугольника, можно вычислить длину третьей стороны, используя эти взаимосвязи.
Используя данные о длинах сторон треугольника, можно также определить, является ли данный треугольник прямоугольным.
Основная теорема геометрии
Теорема Пифагора имеет следующую формулировку: если в треугольнике один угол прямой (равен 90°), то квадрат длины гипотенузы равен сумме квадратов длин двух других сторон.
Эта теорема применяется для проверки существования прямоугольного треугольника. Если известны длины всех трех сторон треугольника, то можно проверить, является ли он прямоугольным, вычислив значения квадратов длин сторон и применив теорему Пифагора.
Формула теоремы Пифагора выглядит следующим образом:
| a2 + b2 = c2 |
Где a и b - длины катетов, а c - длина гипотенузы.
Способы проверки прямоугольности
Для использования теоремы Пифагора необходимо знать длины всех сторон треугольника. Если квадрат длины одной из сторон равен сумме квадратов длин двух других сторон, то треугольник является прямоугольным.
Также можно использовать свойство прямоугольного треугольника, согласно которому сумма квадратов длин катетов равна квадрату длины гипотенузы. Если это свойство выполняется для треугольника, то он является прямоугольным.
Еще одним способом проверки прямоугольности треугольника является использование углов. Если один из углов треугольника равен 90 градусам, то треугольник является прямоугольным.
Важно помнить, что для проверки прямоугольности треугольника необходимо знать длины всех его сторон и/или значения его углов. Использование этих способов позволяет определить, является ли треугольник прямоугольным или нет.
Равенство суммы квадратов катетов гипотенузе

| Катет a: | Катет b: | Гипотенуза c: |
| a2 | b2 | c2 |
То есть, если длины катетов a и b известны, то можно вычислить длину гипотенузы c, применив формулу c = √(a2 + b2). Эта формула позволяет определить, существует ли прямоугольный треугольник с заданными длинами катетов.
Использование углов

Если один из углов треугольника равен 90 градусам, то треугольник является прямоугольным. В таком треугольнике сторона, противолежащая прямому углу, называется гипотенузой, а две другие стороны - катетами.
Для вычисления углов треугольника можно использовать тригонометрические функции: синус, косинус и тангенс. Например, если известны длины двух сторон треугольника, можно вычислить значение угла с помощью тангенса.
Используя эти методы, можно определить, существует ли прямоугольный треугольник. Надо только знать значения углов или длины сторон и быть внимательным при расчетах.
Практические примеры

Рассмотрим несколько практических примеров, которые помогут наглядно понять, как определить существование прямоугольного треугольника:
| Пример | Катет 1 | Катет 2 | Гипотенуза | Результат |
|---|---|---|---|---|
| Пример 1 | 3 | 4 | 5 | Существует |
| Пример 2 | 5 | 12 | 13 | Существует |
| Пример 3 | 6 | 8 | 10 | Существует |
| Пример 4 | 7 | 24 | 25 | Существует |
| Пример 5 | 2 | 3 | 5 | Не существует |
Во всех примерах, где сумма квадратов двух катетов равна квадрату гипотенузы, прямоугольный треугольник существует. Однако, в последнем примере, сумма квадратов двух катетов не равна квадрату гипотенузы, поэтому прямоугольный треугольник не существует.



