Пересечение двух прямых – это одна из самых важных тем в геометрии. Прямые AB и CD могут как пересекаться, так и не пересекаться. Все зависит от их положения и ориентации в пространстве.
Если прямые AB и CD пересекаются, то это означает, что существует точка M, которая одновременно принадлежит обоим прямым. Такая точка называется точкой пересечения. Если точка пересечения существует, то прямые AB и CD считаются пересекающимися.
Если же прямые AB и CD не пересекаются, то это означает, что нет ни одной точки, принадлежащей обеим прямым одновременно. В этом случае говорят, что прямые AB и CD не пересекаются.
Понять, пересекаются ли прямые AB и CD или нет, можно, проведя их на геометрической диаграмме или решив систему уравнений для этих прямых. Нельзя забывать, что каждая прямая определяется двумя точками, и основные сведения о них можно получить, зная координаты этих точек.
Прямые AB и CD: могут ли они пересекаться?

В геометрии прямые могут иметь различные отношения между собой. Существует три основных варианта соотношения прямых: они могут быть параллельными, совпадающими или пересекающимися.
Пересекающиеся прямые имеют точку пересечения, в которой они пересекаются друг с другом. Такая точка может быть единственной или может быть бесконечное количество, в зависимости от вида прямых.
Если прямые AB и CD пересекаются, то они имеют общую точку пересечения, которая указывает на то, что они не являются параллельными или совпадающими. Важно отметить, что пересечение прямых может быть точкой, которая лежит на обеих прямых, или может быть точкой, которая лежит вне обеих прямых.
Определить, пересекаются ли прямые AB и CD, можно с помощью анализа их уравнений. Если уравнение прямой AB и уравнение прямой CD имеют одно и то же решение, то эти прямые пересекаются. Если же решения различны или отсутствуют, прямые AB и CD не пересекаются.
Пересекающиеся прямые могут иметь важное значение в различных областях, включая геометрию, физику и инженерию. Изучение пересекающихся прямых может помочь в анализе и решении различных задач и проблем.
Таким образом, прямые AB и CD могут пересекаться, и это зависит от их уравнений и взаимного расположения в пространстве. Важно проводить анализ и исследование, чтобы определить, пересекаются ли данные прямые или нет.
Рассмотрим геометрическую задачу
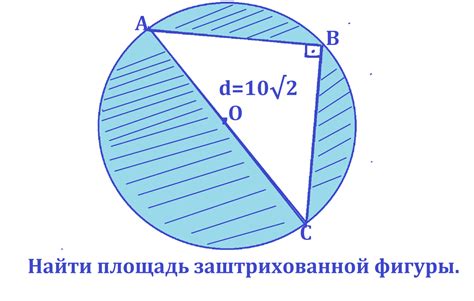
Для решения вопроса о пересечении прямых AB и CD требуется изучить их свойства и взаимное расположение в пространстве.
Прямые могут пересекаться в одной точке, если они не параллельны и не совпадают. В таком случае точка пересечения будет общей для обоих прямых и будет иметь координаты (x, y, z).
Однако, прямые могут быть параллельными и не пересекаться вовсе. В таком случае решение геометрической задачи будет отсутствовать.
Также возможен случай, когда прямые совпадают. В этом случае они будут иметь бесконечное количество точек пересечения.
Основные понятия и определения

Перед тем, как рассматривать вопрос о пересечении прямых AB и CD, следует ознакомиться с некоторыми основными понятиями и определениями из области геометрии:
- Прямая - это геометрическая фигура, которая имеет бесконечную длину и направление. Прямая не имеет начала и конца.
- Отрезок - это часть прямой, ограниченная двумя точками. Отличается от прямой тем, что имеет конечную длину.
- Параллельные прямые - две прямые, которые находятся в одной плоскости и не пересекаются. Они имеют одинаковое направление и расстояние между собой постоянно.
- Пересекающиеся прямые - две прямые, которые пересекаются в точке. Их направления различны, и они имеют одну и только одну общую точку.
- Угол - область плоскости, образованная двумя лучами, имеющими общее начало. Угол измеряется в градусах или радианах и может быть острый, прямой или тупой.
- Вертикальные углы - углы, образованные пересекающимися прямыми и находящиеся противоположно друг другу. Они имеют одинаковую величину.
Понимание этих основных понятий поможет нам разобраться в вопросе о возможности пересечения прямых AB и CD.
Примеры возможных вариантов

Для ответа на вопрос о том, могут ли прямые AB и CD пересекаться, рассмотрим несколько возможных ситуаций:
Вариант 1: Прямые AB и CD параллельны, их направления не пересекаются. В таком случае прямые не пересекаются и не имеют точек пересечения.
Вариант 2: Прямые AB и CD пересекаются в точке P. Это говорит о том, что у прямых AB и CD есть общая точка, в которой они пересекаются друг с другом.
Вариант 3: Прямые AB и CD совпадают. В этом случае прямые пересекаются бесконечное количество раз, так как каждая точка прямой AB будет также являться точкой прямой CD, и наоборот.
Вариант 4: Прямые AB и CD скрещиваются. В этом случае они пересекаются в точке Q и продолжают свое движение в разных направлениях.
Таким образом, прямые AB и CD могут пересекаться или не пересекаться в зависимости от их положения и направления. Каждый из приведенных примеров является возможным вариантом.
Анализ условий пересечения прямых
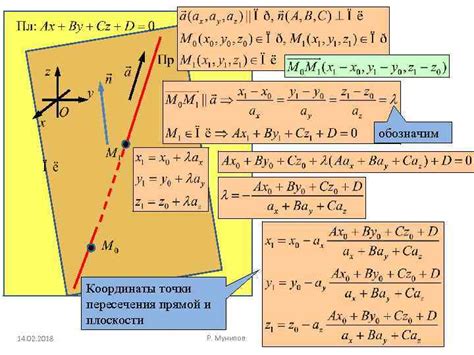
Условия пересечения прямых:
1. Прямые AB и CD могут пересекаться, если они имеют общую точку пересечения. То есть, если существует точка P, которая принадлежит обеим прямым.
Пример:
Если прямая AB задана уравнением y = 2x + 1, а прямая CD задана уравнением y = -x + 3, то точка пересечения P будет удовлетворять обоим уравнениям:
2x + 1 = -x + 3
3x = 2
x = 2/3
Подставляем значение x в одно из уравнений, чтобы найти значение y:
y = 2(2/3) + 1 = 4/3 + 1 = 7/3
Таким образом, точка пересечения P имеет координаты (2/3, 7/3) и прямые AB и CD пересекаются.
2. Прямые AB и CD могут не пересекаться, если они параллельны друг другу. То есть, если угловой коэффициент одной прямой равен угловому коэффициенту другой прямой и они не имеют общей точки пересечения.
Пример:
Если прямая AB задана уравнением y = 3x - 2, а прямая CD задана уравнением y = 3x + 4, то угловые коэффициенты обеих прямых равны 3, но эти прямые не имеют общей точки пересечения. Таким образом, прямые AB и CD параллельны и не пересекаются.
3. Прямые AB и CD могут совпадать, если они имеют одинаковые уравнения и, следовательно, все точки одной принадлежат другой. То есть, если уравнения прямых равны друг другу.
Пример:
Если прямая AB задана уравнением y = x + 2, а прямая CD также задана уравнением y = x + 2, то все точки прямой AB будут принадлежать прямой CD и наоборот. Таким образом, прямые AB и CD совпадают и не имеют точки пересечения, кроме точек, которые принадлежат обеим прямым.
Доказательство возможности пересечения

Для доказательства возможности пересечения прямых AB и CD необходимо анализировать их положение относительно друг друга. Существуют три варианта:
Вариант 1: | Прямые AB и CD параллельны и не пересекаются. |
Вариант 2: | Прямые AB и CD совпадают и пересекаются бесконечное количество раз. |
Вариант 3: | Прямые AB и CD пересекаются в одной точке. |
Для определения положения прямых относительно друг друга можно использовать различные способы, такие как определение угла наклона, использование уравнений прямых и т. д.



