В мире математики существует множество правил и законов, которые определяют теорию чисел и их взаимосвязь. Одним из таких вопросов является возможность деления неравенств в математике. Многие ученики часто задаются вопросом: можно ли делить неравенство на неравенство и получить правильное математическое утверждение? Давайте разберемся.
Первое, что следует отметить, это тот факт, что математика строится на строгих и четких правилах. Поэтому, прежде чем делить неравенство на неравенство, мы должны установить, что такое действие допустимо в рамках математической системы.
В математике существует аксиома, которая гласит: «Если a, b и c являются произвольными числами, и a > b, то a + c > b + c». Эта аксиома говорит нам о том, что мы можем добавить одно и то же число к обеим сторонам неравенства и сохранить его свойства. Однако, аксиома не дает нам право делить неравенство на неравенство безопасно.
Когда мы делим неравенство на неравенство, например a/b > c/d, мы должны быть осторожны. В отличие от сложения и вычитания, деление на неравенство может привести к потере некоторых свойств неоравенства. В результате этой операции, мы можем получить недействительное утверждение.
Определение деления неравенств

Во-первых, при делении неравенств нужно быть осторожным, так как неравенство может измениться. Если оба члена неравенства положительные, то неравенство сохраняет свой знак после деления. Но когда оба члена неравенства отрицательные, знак должен быть изменен.
Во-вторых, при делении неравенство на отрицательное число, необходимо помнить, что направление неравенства также должно измениться.
Возможность деления неравенств в математике

При решении математических задач возникает вопрос о том, можно ли делить неравенство на неравенство. Ответ на этот вопрос зависит от условий, которые заданы в неравенстве.
Если обе стороны неравенства положительны или отрицательны, то деление неравенства на неравенство допустимо. Например, если дано неравенство: a > b и c > d, то можно безопасно поделить обе стороны неравенства на c и получить выражение a/c > b/d.
Однако, если хотя бы одна сторона неравенства является нулем или отрицательным числом, то деление неравенства на неравенство не возможно. Например, если дано неравенство: a > b и c < 0, то нельзя поделить обе стороны неравенства на c.
Таким образом, при решении математических задач необходимо учитывать условия и ограничения, заданные в неравенстве, чтобы определить, можно ли делить неравенство на неравенство.
Правила деления неравенств
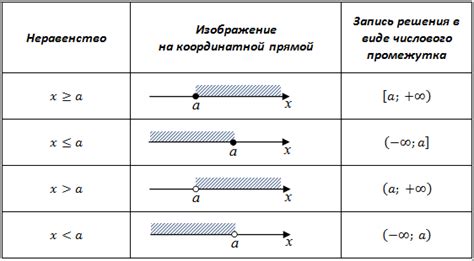
При решении математических задач часто встает вопрос о возможности деления неравенств. Ответ на этот вопрос зависит от определенных правил, которые следует учитывать при выполнении таких операций.
Основное правило гласит, что если обе части неравенства (левая и правая) положительны или отрицательны, то неравенство можно разделить на это число без изменения знака. Например:
| Исходное неравенство | Результат деления |
|---|---|
| x > 3 | x/3 > 1 |
| y < -2 | y/(-2) < 1 |
Однако, если знаки разных частей неравенства различаются (одна положительная, другая отрицательная), то нельзя делить неравенство на это число без изменения знака. В данном случае требуется изменить направление неравенства. Например:
| Исходное неравенство | Результат деления |
|---|---|
| x > 2 | -x < -1 |
| y < -5 | -y > 3 |
Также стоит помнить, что если при делении неравенства на отрицательное число происходит изменение знака, то таким же образом нужно изменить направление неравенства. Например:
| Исходное неравенство | Результат деления |
|---|---|
| x > -4 | x/(-4) < 1 |
| y < -3 | y/3 > -1 |
Таким образом, правила деления неравенств в математике позволяют нам выполнять операции с неравенствами, сохраняя их корректность и справедливость.
Примеры деления неравенств

- Пример 1:
Если дано неравенство 2x + 3 > 7, чтобы найти значение переменной x, можно сначала вычесть 3 с обеих сторон неравенства: 2x + 3 - 3 > 7 - 3, что дает 2x > 4. Затем можно разделить обе части неравенства на 2, чтобы найти значения переменной: 2x/2 > 4/2, что приводит к x > 2. - Пример 2:
Если дано неравенство 4x - 5 < 3, чтобы найти значение переменной x, можно сначала прибавить 5 к обеим сторонам неравенства: 4x - 5 + 5 < 3 + 5, что дает 4x < 8. Затем можно разделить обе части неравенства на 4, чтобы найти значения переменной: 4x/4 < 8/4, что приводит к x < 2. - Пример 3:
Если дано неравенство 3x/2 ≥ 9, чтобы найти значение переменной x, можно сначала умножить обе стороны неравенства на 2/3: (3x/2)*(2/3) ≥ 9*(2/3), что дает x ≥ 6.
Итак, эти примеры показывают, что в некоторых случаях можно делить неравенства на неравенства, но необходимо быть осторожным и соблюдать определенные правила и условия.
Ограничения при делении неравенств

При работе с неравенствами в математике, деление неравенства на неравенство может иметь определенные ограничения. Во-первых, необходимо помнить, что при делении неравенства на отрицательное число, направление неравенства будет меняться.
Следует помнить, что если все элементы неравенства отрицательны, то при делении неравенства на неравенство направление неравенства будет меняться.
При делении на переменную, необходимо учесть, что если переменная может принимать отрицательные значения, то направление неравенства будет меняться в зависимости от знака переменной.
Также стоит отметить, что при делении неравенств можно столкнуться с делением на ноль. В данном случае, результат будет неопределенным, и деление неравенств нельзя будет выполнить.
Важно проводить анализ и учитывать все возможные ограничения при делении неравенств, чтобы не допустить ошибок и получить корректные результаты.
При анализе возможности деления неравенств в математике было выяснено, что общепринятое правило гласит: "Если оба члена неравенства положительны или отрицательны, можно делить неравенство на положительное число". Однако, необходимо быть осторожным при использовании этого правила, так как при делении неравенств на отрицательные числа знак неравенства должен быть изменен.
Если один из членов неравенства равен нулю, то деление неравенства на это число будет недопустимо, поскольку в математике невозможно делить на ноль.
Таким образом, важно помнить о правилах и осторожно применять деление неравенств в математике, чтобы избежать ошибок и получить правильные результаты.+



