Матрицы - это одна из важных концепций линейной алгебры, которая находит широкое применение в различных областях, включая физику, компьютерную графику и экономику. Вопрос о том, можно ли складывать матрицы разного размера, является актуальным и важным для понимания основ матричной алгебры.
В общем случае, сложение матриц возможно только в том случае, если они имеют одинаковый размер. Однако, в некоторых особых случаях, складывать матрицы разного размера также является допустимым.
Например, если матрицы имеют разное количество столбцов, но одинаковое количество строк, то их можно сложить путем сложения соответствующих элементов. Получившаяся матрица будет иметь тот же размер, что и исходные матрицы.
Однако, если матрицы имеют разное количество строк, то сложение невозможно. В этом случае говорят, что матрицы несовместимы для сложения.
Возможность сложения матриц разного размера
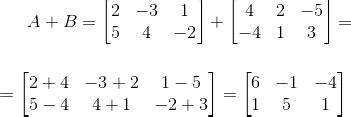
Матрицы могут быть сложены только в случае, если они имеют одинаковые размеры, то есть одинаковое количество строк и столбцов. В противном случае, сложение матриц не определено и невозможно выполнить.
Если же матрицы имеют разные размеры, их нельзя просто сложить. В таком случае, можно рассмотреть другие операции над матрицами, такие как умножение или транспонирование.
Если требуется сложить матрицы разного размера, необходимо изменить их размеры таким образом, чтобы количество строк и столбцов совпадало. Это можно сделать путем добавления нулевых элементов или удаления некоторых строк и столбцов. Однако, при таком изменении размеров матриц, может измениться и смысл операции сложения.
Сложение матриц равного размера

При сложении матриц элементы с одинаковыми индексами складываются поэлементно. Полученная матрица будет иметь тот же размер, что и исходные матрицы. Например, если имеем матрицы A и B размером nxm, их сумма будет представлена матрицей C размером nxm, где каждый элемент Ci,j будет равен сумме соответствующих элементов матриц A и B: Ci,j = Ai,j + Bi,j.
Сложение матриц равного размера может быть применено, например, для сложения векторов или для выполнения операций над пикселями изображения.
| Матрица A | Матрица B | Матрица C (A + B) |
|---|---|---|
| a1,1 | b1,1 | c1,1 = a1,1 + b1,1 |
| a1,2 | b1,2 | c1,2 = a1,2 + b1,2 |
| a2,1 | b2,1 | c2,1 = a2,1 + b2,1 |
| a2,2 | b2,2 | c2,2 = a2,2 + b2,2 |
Таким образом, сложение матриц разного размера невозможно, а сложение матриц равного размера выполняется путем поэлементного сложения соответствующих элементов исходных матриц.
</p>
Сложение матриц разного размера с помощью дополнения нулями
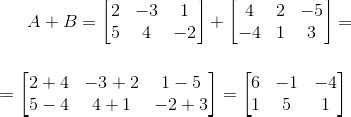
В таком случае можно воспользоваться методом дополнения нулями. Суть этого метода заключается в том, что матрица меньшего размера преобразуется путем добавления нулей в конец строк или столбцов до размеров матрицы большего размера.
Таким образом, при сложении матриц разного размера с помощью дополнения нулями, сначала следует привести обе матрицы к одному размеру, а затем сложить соответствующие элементы каждой матрицы. При этом элементы, которые соответствуют нулевым добавленным элементам, будут равны нулю.
Примером может служить сложение двух матриц размерами 3x3 и 2x2:
- Матрица A:
- 1 2 3
- 4 5 6
- 7 8 9
- Матрица B:
- 1 2
- 3 4
Для выполнения сложения матрицы B необходимо преобразовать, добавив нулевой элемент в конец каждой строки:
- Матрица B:
- 1 2 0
- 3 4 0
Теперь можно выполнить сложение матриц A и B:
- Результат сложения:
- 2 4 3
- 7 9 6
- 7 8 9
Сложение матриц разного размера с помощью использования подматрицы

Обычно сложение матриц возможно только в случае, если они имеют одинаковые размеры. Однако, существует способ сложить матрицы разного размера, используя подматрицы. Подматрицей называется матрица, полученная из исходной матрицы путем выбора некоторых элементов.
Для сложения матриц разного размера с помощью подматрицы необходимо произвести следующие действия:
- Выбрать подматрицу из каждой исходной матрицы. Это должна быть общая область элементов, то есть они должны иметь одинаковые координаты в обеих матрицах.
- Сложить выбранные подматрицы поэлементно.
- Полученные значения помещаются в соответствующие позиции новой матрицы, которая будет иметь размер, соответствующий размеру выбранных подматриц.
- Все оставшиеся элементы новой матрицы заполняются нулями или произвольными значениями.
Сложение матриц разного размера с помощью использования подматрицы позволяет получать результат, объединяющий информацию из исходных матриц, даже если их размеры отличаются. Однако, при этом, размер полученной матрицы будет определяться размером выбранных подматриц, поэтому необходимо быть внимательным при выборе подматрицы, чтобы информация не терялась.



