Квадраты в уравнении – это часто встречающаяся тема в математике, которую многие ученики и студенты считают сложной и запутанной. Вопрос о возможности сокращения квадратов в уравнении является одним из наиболее распространенных и часто задаваемых.
Конечно, можно сокращать квадраты в уравнении! Однако, необходимо придерживаться определенных правил и методов для правильного применения этой операции. Неосторожное сокращение квадратов может привести к ошибкам и неправильным решениям.
Давайте рассмотрим пример. Предположим, у нас есть уравнение x^2 + 4x + 4 = 0. Здесь мы видим квадратный член x^2 и линейный член 4x, которые можно сократить. Мы можем записать это уравнение в виде (x + 2)^2 = 0. Теперь мы видим, что у нас есть квадратный трехчлен, который равен нулю.
Однако есть важное замечание: сокращением мы не убираем квадратный член из уравнения, мы просто записываем его в другой форме. Это означает, что сокращение квадратов не изменяет суть уравнения и его решений. В данном примере, решением уравнения будет x = -2.
Таким образом, взяв за основу определенные методы и правила, мы можем успешно сокращать квадраты в уравнении и упрощать его запись. Практика и понимание этих методов помогут вам в решении сложных уравнений и получении правильных ответов.
Можно ли сокращать квадраты в уравнении?

Когда можно сокращать квадраты в уравнении? Это является возможным, если уравнение имеет вид квадратного трехчлена или можно преобразовать его к данному виду.
Например, рассмотрим уравнение x^2 + 2x + 1 = 0. Здесь квадратный трехчлен x^2 имеет коэффициенты 1, 2 и 1. Мы можем представить этот квадратный трехчлен в виде (x + 1)^2 и значит сократить его, получив (x + 1)(x + 1) = 0. Затем мы можем решить уравнение приравняв каждый множитель к нулю: x + 1 = 0, что дает нам корень x = -1.
Однако, стоит отметить, что в общем случае, сокращение квадратов в уравнении недопустимо, поскольку это может привести к потере корней и неверным решениям. Поэтому, при решении уравнений, всегда следует тщательно анализировать структуру и свойства уравнения, прежде чем применять сокращение квадратов.
Квадратные уравнения: определение и примеры

Для решения квадратного уравнения можно использовать квадратное уравнение вида x^2 = d, где d - некоторое число. Затем применяется операция извлечения квадратного корня для нахождения значений переменной. Если вместо d вступает отрицательное число, то квадратное уравнение не имеет решения в действительных числах, но имеет решение в комплексных числах, обозначаемых как a + bi, где a и b - это вещественные числа, а i - мнимая единица (i^2 = -1).
Примеры квадратных уравнений:
1. x^2 + 5x + 6 = 0
2. 2x^2 - 3x - 2 = 0
3. 3x^2 + 7x - 4 = 0
Решение этих уравнений можно получить путем применения формулы дискриминанта, которая позволяет найти значения переменной x. Дискриминант вычисляется по формуле D = b^2 - 4ac, где b, a и c - коэффициенты квадратного уравнения.
Затем, в зависимости от значения дискриминанта, можно определить количество решений:
- Если D > 0, то уравнение имеет два разных решения.
- Если D = 0, то уравнение имеет одно решение.
- Если D < 0, то уравнение не имеет решений в действительных числах.
Важно отметить, что сокращение квадратов в уравнении неправильным способом может привести к некорректным результатам, поэтому важно правильно применять математические операции при решении квадратных уравнений.
Квадратное уравнение без сокращения: пример решения

Рассмотрим пример. Дано квадратное уравнение 3x^2 + 5x + 2 = 0. Чтобы найти решение, нужно сначала определить значения a, b и c.
В данном случае, a = 3, b = 5 и c = 2.
Далее, чтобы решить уравнение, мы можем использовать формулу дискриминанта D = b^2 - 4ac.
Подставим значения коэффициентов в формулу дискриминанта: D = 5^2 - 4*3*2 = 25 - 24 = 1.
Поскольку значение дискриминанта положительное, уравнение имеет два действительных корня.
Далее, мы можем использовать формулы для нахождения корней квадратного уравнения:
Первый корень: x1 = (-b + √D) / (2a) = (-5 + √1) / (2*3) = (-5 + 1) / 6 = -4/6 = -2/3.
Второй корень: x2 = (-b - √D) / (2a) = (-5 - √1) / (2*3) = (-5 - 1) / 6 = -6/6 = -1.
Таким образом, квадратное уравнение 3x^2 + 5x + 2 = 0 имеет два действительных корня: -2/3 и -1.
Как сократить квадраты в уравнении: основные правила
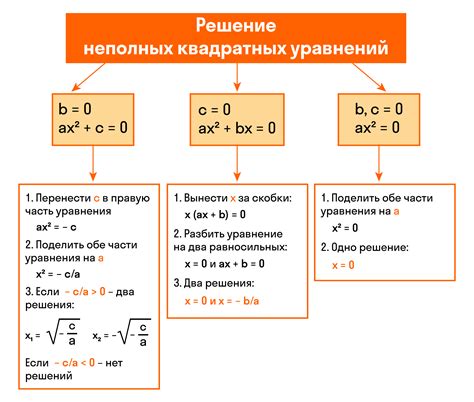
1. Разность квадратов: Если в уравнении имеется разность квадратов, то ее можно сократить, используя формулу (a^2 - b^2) = (a+b)(a-b). Например, если имеется уравнение x^2 - 9 = 0, то мы можем записать его как (x+3)(x-3) = 0.
2. Сумма квадратов: В случае, если у нас есть сумма квадратов, то можно сократить ее, используя формулу (a^2 + b^2) = (a+b)(a-b). Например, если имеется уравнение x^2 + 4 = 0, то мы можем записать его как (x+2i)(x-2i) = 0, где i – мнимая единица.
3. Квадратичные трехчлены: В случае, когда имеется квадратичный трехчлен вида ax^2 + bx + c = 0, можно сократить квадраты, применив формулу сокращения квадратов. Для этого нужно проверить, можно ли представить уравнение в таком виде: (px + q)^2 = 0. Если это возможно, то уравнение может быть сокращено до (px + q) = 0.
4. Квадраты с вещественными числами: Если повсюду появляются квадратные корни в уравнении, то можно сократить квадраты, применяя формулу извлечения корней (a^2)^(1/2) = a. Например, если имеется уравнение (x^2)^(1/2) + 1 = 0, то мы можем записать его как x + 1 = 0.
Это лишь несколько основных правил и примеров того, как можно сокращать квадраты в уравнении. С помощью этих техник и формул можно значительно упростить уравнение и найти его решение. Важно помнить, что каждое уравнение уникально и требует индивидуального подхода при его решении.
Примеры сокращения квадратов в уравнении

Когда решаем уравнения, содержащие квадраты, иногда можно сократить эти квадраты для упрощения выражений. Вот несколько примеров сокращения квадратов в уравнениях:
Пример 1:
Рассмотрим уравнение: $x^2 + 6x + 9 = 0$. Здесь мы видим, что первый и третий члены - это квадраты ($x^2$ и $9 = 3^2$). Мы также замечаем, что сумма первого и второго члена составляет квадрат ($x^2 + 6x = (x + 3)^2$). Поэтому, мы можем записать уравнение в виде: $(x + 3)^2 = 0$. Это даёт нам решение: $x = -3$.
Пример 2:
Рассмотрим уравнение: $4x^2 + 12x + 9 = 0$. Здесь мы видим, что третий член - это квадрат ($9 = 3^2$). Мы также замечаем, что первый и второй члены можно представить в виде квадрата ($4x^2 + 12x = (2x + 3)^2$). Поэтому, мы можем записать уравнение в виде: $(2x + 3)^2 = 0$. Это даёт нам решение: $x = -\frac{3}{2}$.
Пример 3:
Рассмотрим уравнение: $9x^2 - 12x + 4 = 0$. Здесь мы видим, что последний член - это квадрат ($4 = 2^2$). Мы также замечаем, что первый и второй члены можно представить в виде квадрата ($9x^2 - 12x = (3x - 2)^2$). Поэтому, мы можем записать уравнение в виде: $(3x - 2)^2 = 0$. Это даёт нам решение: $x = \frac{2}{3}$.
Таким образом, сокращение квадратов в уравнениях может помочь упростить выражения и найти решения.
Почему нельзя всегда сокращать квадраты в уравнении?

Квадраты нельзя сокращать в уравнении по следующим причинам:
1. Разные переменные: Если в уравнении присутствуют различные переменные, то нельзя сокращать их квадраты. Например, в уравнении x^2 + y^2 = 25, нельзя проводить сокращение квадратов переменных x и y, так как они представлены разными символами и относятся к разным значениям.
2. Разные степени: Если в уравнении присутствуют переменные с разными степенями, то также нельзя сокращать квадраты. Например, в уравнении x^2 + x = 6, нельзя проводить сокращение квадрата переменной x, так как она представлена с переменной с линейной степенью.
3. Несократимые выражения: В некоторых случаях часть уравнения может представлять несократимые выражения, в которых нельзя сокращать квадраты. Например, в уравнении (x - 4)^2 + 9 = 25, необходимо рассматривать всё выражение (x - 4)^2 как одно целое и не проводить сокращение.
Обратите внимание, что сокращение квадратов возможно только в случае, когда квадратные выражения имеют одинаковые переменные и одинаковые степени.
Знание о правилах сокращения и невозможности сокращения квадратов в уравнении позволяет избежать ошибок при решении математических задач и достигнуть точных результатов.
Как определить, нужно ли сокращать квадраты в уравнении?

В процессе решения уравнений, часто возникает вопрос о необходимости сокращения квадратов. Сокращение квадратов в уравнении может быть полезным при упрощении или получении более простого вида уравнения. Однако, не всегда целесообразно проводить данное действие, и в некоторых случаях оно даже может ввести в заблуждение.
Для определения, нужно ли сокращать квадраты в уравнении, следует рассмотреть его структуру и задачу, которую требуется решить. При анализе уравнения, необходимо обратить внимание на наличие квадратных корней, вкладывающих особую информацию о возможных решениях.
Если уравнение имеет вид a2 + b2 = c2, где a, b и c – это выражения, содержащие переменные или константы, то сокращение квадратов может оказаться полезным. В этом случае можно применить такое преобразование: (a + b)(a - b) = c2.
Однако, если уравнение имеет форму a2 - b2 = c или a2 + b2 = c, то квадраты нельзя сокращать. В этих случаях, сокращение может привести к неправильным результатам или даже к отсутствию решений.
При решении уравнений с квадратами, всегда целью является получение простой и понятной формы уравнения. Если сокращение квадратов помогает достичь этой цели и не нарушает правила математики, то оно может быть использовано. Однако, важно быть осторожным и аккуратным в процессе сокращения, чтобы не потерять важные решения или создать новые ошибки.



