Вернуться к квадратному номеру - это вопрос, который интересует множество людей. Можно ли вернуться к прежней форме и ощущениям? Квадратный номер, или квадрат прежнего числа, - это число, полученное путем умножения числа на себя. Например, квадратный номер числа 5 равен 25.
Вернуться к квадратному номеру может быть сложно, но это возможно, если принять правильные практические рекомендации. Важно помнить, что каждый человек индивидуален, и то, что работает для одного, может не сработать для другого. Однако, есть несколько общих советов, которые могут помочь в этом процессе.
Во-первых, для возвращения к квадратному номеру важно уделить внимание своему физическому здоровью. Регулярные физические упражнения и здоровое питание помогут укрепить ваше тело и повысить общую выносливость. Кроме того, они помогут улучшить ваше самочувствие и настроение, что важно для достижения поставленных целей.
Квадратный номер - всё, что вы должны знать

Важно отметить, что квадратные номера имеют много интересных свойств и применений. Они используются в различных областях науки, технологии и инженерии.
Одно из основных применений квадратных номеров - решение уравнений. Квадратные номера часто появляются при решении квадратных уравнений. Например, при решении уравнения x^2 - 9 = 0, мы получаем квадратные номера x = 3 и x = -3.
Квадратные номера также используются для измерения площадей и объемов. Например, если у вас есть квадрат со стороной 3 см, то его площадь будет равна 3^2 = 9 квадратным сантиметрам. А если у вас есть куб со стороной 3 см, то его объем будет равен 3^3 = 27 кубическим сантиметрам.
Кроме того, квадратные номера используются в графиках и геометрии. Например, если у вас есть точка на плоскости с координатами (3, 4), то квадратное число этой точки будет равно 3^2 + 4^2 = 9 +16 = 25.
Интересно отметить, что квадратный номер может быть как положительным, так и отрицательным. Чтобы получить квадратный номер -9, достаточно возвести в квадрат число -3. Таким образом, (-3)^2 = 9 и -3^2 = -9.
Квадратный номер: определение и свойства

Квадратные числа обладают несколькими интересными свойствами:
- Квадратные числа являются всегда положительными, так как квадрат любого числа не может быть отрицательным.
- Все натуральные числа, являющиеся квадратами, имеют нечетное количество делителей. Например, число 9 имеет делители 1, 3 и 9, а квадраты простых чисел имеют всего два делителя - 1 и само число.
- Квадратные числа образуют последовательность, где каждое следующее число равно сумме предыдущего числа и нечетного числа. Например, 1 + 3 = 4, 4 + 5 = 9, 9 + 7 = 16 и так далее.
- Квадратные числа могут быть представлены в виде фигур, называемых квадратами, с равными сторонами.
Знание свойств квадратных чисел может быть полезным для решения различных математических задач и позволяет лучше понять мир чисел и их взаимосвязи.
Зачем нужны квадратные номера в математике

1. Вычисления площади:
Квадратные числа помогают в вычислении площади различных фигур, таких как квадраты и прямоугольники. Площадь можно выразить как квадрат числа, которое представляет длину стороны фигуры.
2. Описание движения:
Квадратные числа можно использовать для описания движения в физических процессах. Они помогают нам понять и предсказать, как объект будет перемещаться в зависимости от времени и других факторов.
3. Решение квадратных уравнений:
Квадратные числа тесно связаны с квадратными уравнениями. Они позволяют нам решать такие уравнения и находить значения переменных. Кроме того, они имеют много приложений в физике и инженерии.
4. Понимание квадратного корня:
Квадратные числа нам также помогают понять понятие квадратного корня. Каждое квадратное число имеет его квадратный корень, который является положительным числом, возведенным в квадрат и давшим исходное число.
Плюсы и минусы использования квадратных номеров

Плюсы использования квадратных номеров:
- Уникальность: каждый квадратный номер имеет уникальный идентификатор, что делает их удобными для ссылки и поиска конкретного объекта или явления.
- Легкость использования: квадратные номера легко читать и запоминать, особенно при использовании простых и понятных шаблонов.
- Структурированность: квадратные номера могут представлять определенную структуру или классификацию, что помогает в организации информации.
- Гибкость: при необходимости можно изменить или расширить систему квадратных номеров, добавив новые элементы или используя дополнительные символы.
Минусы использования квадратных номеров:
- Ограничения в количестве: в системе квадратных номеров может быть ограниченное количество доступных комбинаций, что может стать проблемой при большом количестве объектов или явлений.
- Необходимость обновления: при изменении объектов или явлений может потребоваться обновление квадратных номеров, что может быть трудоемким и затратным процессом.
- Подверженность ошибкам: при ручном создании или вводе квадратных номеров может возникать ошибка, что может привести к неправильной идентификации объектов или явлений.
- Неоднозначность: в некоторых случаях квадратные номера могут быть неоднозначными, особенно если они имеют общий шаблон или структуру с другими номерами.
При использовании квадратных номеров необходимо тщательно взвесить все плюсы и минусы и учесть специфику и требования вашего проекта или организации.
Как вычислить квадратный номер
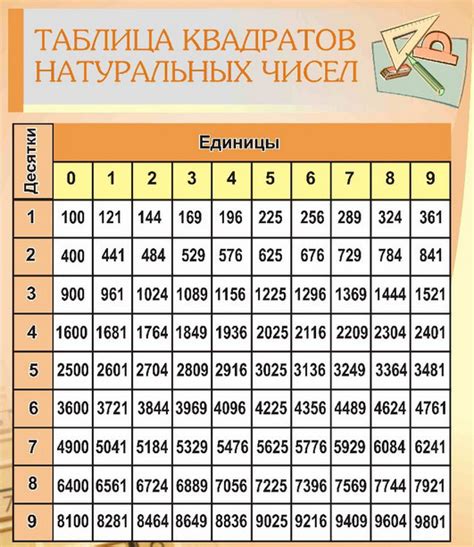
Квадратный номер можно вычислить, умножая число на само себя.
Для вычисления квадратного номера числа, необходимо его возвести в квадрат. Для этого можно использовать операцию умножения.
Пример:
Допустим, нам нужно вычислить квадратный номер числа 7. Для этого нужно число 7 возвести во вторую степень: 7 * 7 = 49. Таким образом, квадратный номер числа 7 равен 49.
Каким бы ни было число, его квадратный номер всегда будет положительным. Например, квадратный номер числа -5 равен 25.
Важно помнить! Вычисление квадратного номера есть простой способ найти площадь квадрата со стороной, равной заданному числу.
Также следует заметить, что операция возведения в квадрат является обратной операцией к извлечению квадратного корня.
Пример:
Если квадратный номер числа равен 25, то извлекая из него квадратный корень, мы получим число 5, так как 5 * 5 = 25.
В вычислении квадратного номера нет ничего сложного. Важно только не перепутать понятия и использовать правильные математические операции.
Практические рекомендации по использованию квадратного номера

1. Математические вычисления:
Квадратный номер может быть использован для выполнения различных математических операций, таких как извлечение квадратного корня и возведение в квадрат. Например, если вам нужно найти квадратный корень числа, вы можете использовать квадратный номер для выполнения этой операции.
2. Формулы и уравнения:
Квадратный номер может быть использован для решения уравнений и формул. Он может помочь вам найти значения переменных или решить сложные математические задачи. Например, в физике вы можете использовать квадратный номер для решения уравнений движения.
3. Геометрия:
Квадратный номер также может быть полезен в геометрии. Он может помочь в вычислении площадей и периметров квадратов, прямоугольников и других фигур. Например, вы можете использовать квадратный номер для вычисления площади квадрата по его стороне.
4. Программирование:
В программировании квадратный номер может быть использован для генерации случайных чисел или управления выполнением кода. Он может помочь в создании алгоритмов и определении условий выполнения программы. Например, вы можете использовать квадратный номер для генерации случайных координат в игре.
Использование квадратного номера может помочь в решении различных задач и упростить математические вычисления. Не стесняйтесь использовать этот полезный инструмент в своей работе или учебе!
Примеры использования квадратных номеров в жизни

Квадратные номера имеют широкое применение в жизни и смогут быть полезными в различных областях. Рассмотрим несколько примеров:
1. Пометка страниц в книге.
Квадратный номер может быть использован для пометки страниц в книге. Например, вы можете оставить квадратный номер возле важной страницы, чтобы быстро найти ее в дальнейшем.
2. Градуировка линейки.
Квадратные номера могут быть использованы для градуировки линейки или измерительного инструмента. Например, вы можете указать квадратные номера на линейке каждый десятый деление для удобства измерений.
3. Пронумеровывать задачи в задании.
Если у вас есть список задач или упражнений, квадратные номера могут помочь в пронумеровывании каждой задачи. Это облегчит отслеживание выполненных и не выполненных задач.
4. Разметка учебного материала.
Квадратные номера могут быть использованы для разметки учебного материала, например, для выделения ключевых понятий или определений. Это поможет вам быстро найти нужную информацию и повысит эффективность обучения.
5. Определение приоритетности задач.
Вы также можете использовать квадратные номера для определения приоритетов задач. Например, можно пронумеровать задачи в порядке важности или срочности, чтобы было ясно, какие задачи нужно выполнить в первую очередь.
Мифы и заблуждения о квадратных номерах

Существует множество мифов и недоразумений вокруг квадратных номеров, которые могут ввести в заблуждение. Рассмотрим некоторые из них:
Миф: Все числа могут иметь квадратный номер.
Факт: Квадратный номер существует только для неотрицательных чисел. Отрицательные числа не имеют квадратного номера. Например, квадратный корень из -9 не определен.
Миф: Квадратный номер всегда положителен.
Факт: Квадратный номер может быть как положительным, так и нулевым. Например, квадратный корень из 0 равен 0.
Миф: Квадратный номер всегда целое число.
Факт: Квадратный номер может быть как целым, так и дробным числом. Например, квадратный корень из 2 равен примерно 1.414.
Миф: Квадратный номер всегда рациональное число.
Факт: Квадратный номер может быть как рациональным, так и иррациональным числом. Например, квадратный корень из 2 является иррациональным числом.
Миф: Квадратный номер всегда единственный.
Факт: У каждого положительного числа есть два квадратных корня: один положительный и один отрицательный. Например, квадратный корень из 9 равен 3 или -3.
Познакомившись с реальными фактами о квадратных номерах, вы сможете более точно использовать их в практике и избежать попадания в заблуждение.
Потенциал и перспективы квадратных номеров

Основной потенциал квадратных номеров заключается в их уникальности и удобстве использования. Каждый квадратный номер имеет свой уникальный идентификатор, который позволяет с легкостью отслеживать, идентифицировать и описывать определенные элементы или объекты.
Квадратные номера могут быть использованы в различных областях, таких как научные исследования, инженерия, архитектура, информационные технологии, логистика и многие другие. В научных исследованиях они могут помочь в однозначной идентификации и систематизации данных и результатов. В инженерии и архитектуре они позволяют эффективно классифицировать и описывать элементы и строения. В информационных технологиях и логистике они упрощают процессы и распределение ресурсов.
Использование квадратных номеров также облегчает коммуникацию и взаимодействие между специалистами в разных областях деятельности. Благодаря однозначному кодированию и классификации элементов, специалисты могут быстро обмениваться информацией и легко понимать друг друга.
Будущие перспективы квадратных номеров связаны с развитием их использования в новых областях, а также с автоматизацией процессов их применения. Технологии распознавания и идентификации позволяют все более эффективно использовать квадратные номера для автоматического анализа и классификации данных.
В целом, квадратные номера являются важным инструментом для систематизации, идентификации и классификации элементов в различных областях деятельности. Их потенциал и перспективы только возрастают, делая их неотъемлемой частью современного мира.



