Коэффициент корреляции – это одна из наиболее распространенных мер статистической связи между двумя переменными. Он позволяет оценить, насколько сильно и в каком направлении связаны две случайные величины. Суть коэффициента корреляции заключается в измерении степени линейной зависимости между двумя переменными.
В случае сильной значимой корреляционной связи коэффициент корреляции стремится к единице и имеет положительное или отрицательное значение. Это означает, что две переменные движутся в одном направлении и связаны друг с другом с большой силой.
Однако, важно отметить, что сильная значимая корреляционная связь не означает причинно-следственную связь между переменными. Коэффициент корреляции позволяет лишь оценить статистическую связь, но не является доказательством причинности.
Особенности и значение сильной значимой корреляционной связи

Сильная значимая корреляционная связь – это тесная и статистически значимая связь между двумя переменными. Она означает, что изменение значения одной переменной сопровождается предсказуемым изменением значения другой переменной.
При наличии сильной значимой корреляционной связи коэффициент корреляции будет близким к 1 или -1. Если корреляция близка к 1, это говорит о прямой связи между переменными – увеличение значения одной переменной сопровождается увеличением другой переменной. Если корреляция близка к -1, это означает обратную связь – увеличение значения одной переменной сопровождается уменьшением значения другой переменной.
Значимость корреляционной связи оценивается с помощью p-значения. Если p-значение меньше установленного порогового значения (например, 0,05), корреляционная связь считается статистически значимой.
Значение сильной значимой корреляционной связи заключается в том, что она позволяет нам прогнозировать значения одной переменной на основе значений другой переменной. Это может быть полезно при проведении исследований, анализе данных и принятии решений, особенно в научных и бизнес-сферах.
Понятие и суть корреляции

Корреляция измеряется с помощью коэффициента корреляции, который принимает значения от -1 до 1. Значение -1 означает полную отрицательную корреляцию, 1 – положительную корреляцию, а 0 – отсутствие корреляции. Чем ближе значение коэффициента корреляции к 1 или -1, тем сильнее связь между переменными. Значение 0 говорит о том, что переменные не связаны между собой.
Корреляция может быть линейной или нелинейной. Линейная корреляция предполагает, что связь между переменными может быть аппроксимирована прямой линией или ее аналогом. Нелинейная корреляция возникает, когда связь имеет другую форму, например, квадратичную или экспоненциальную.
Корреляция может использоваться для различных целей. Она может помочь выявить причинно-следственную связь между переменными, предсказать значения одной переменной на основе значений другой переменной, а также определить силу и направление связи между переменными.
Значение коэффициента корреляции

Значение коэффициента корреляции может варьироваться от -1 до 1. Положительное значение коэффициента указывает на прямую линейную связь между переменными, так что при увеличении значений одной переменной значения другой переменной также увеличиваются. Отрицательное значение коэффициента корреляции указывает на обратную линейную связь, при которой увеличение значений одной переменной сопровождается уменьшением значений другой переменной.
Чем ближе значение коэффициента корреляции к 1 или -1, тем сильнее связь между переменными. Значения близкие к 0 говорят о слабой связи. Существуют различные шкалы для интерпретации величины коэффициента корреляции, однако общепринятой нормы для определения сильной значимой связи не существует. Оценка силы связи должна основываться на конкретной предметной области и цели исследования.
Однако следует помнить, что коэффициент корреляции не является причинно-следственной связью. Он лишь показывает наличие статистической связи между переменными и ее степень, но не указывает на то, какое из двух явлений является причиной, а какое следствием.
Важно также отметить, что коэффициент корреляции подходит только для оценки линейной связи между переменными. Если имеется нелинейная связь, то коэффициент корреляции может давать искаженные или неполные результаты. В таких случаях требуется использование других методов и оценок для анализа связи между переменными.
Сильная и значимая корреляционная связь

Однако, для того чтобы быть уверенными в существовании сильной и значимой связи, необходимо применять статистические методы. При анализе данных мы оцениваем среднее значение коэффициента корреляции и его стандартное отклонение. Далее, при помощи статистических тестов мы определяем, является ли полученный коэффициент корреляции статистически значимым.
Если полученный коэффициент корреляции является сильным (близким к 1 или -1) и статистически значимым, то можно говорить о существовании сильной и значимой корреляционной связи между переменными. Сильная и значимая связь означает, что изменение одной переменной сопровождается предсказуемым изменением другой переменной.
Особенности коэффициента корреляции
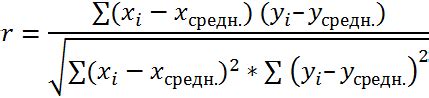
Первая особенность связана с тем, что коэффициент корреляции может принимать значения только в диапазоне от -1 до 1. Если значение коэффициента равно 1, то это означает, что между переменными существует положительная линейная связь, а если значение равно -1, то связь является отрицательной. Значение 0 указывает на отсутствие линейной связи.
Вторая особенность состоит в том, что коэффициент корреляции не является причинно-следственной связью. Это означает, что, хотя между переменными может существовать сильная корреляционная связь, это не означает, что одна переменная причиняет изменения в другой переменной.
Третья особенность заключается в том, что коэффициент корреляции измеряет только линейную связь между переменными. Если между переменными существует нелинейная связь, то коэффициент корреляции может быть недостаточно информативным.
Поэтому, при интерпретации коэффициента корреляции необходимо учитывать его значения, причинно-следственные связи и возможность нелинейной связи между переменными. Только так можно получить полное представление о взаимосвязи между двумя переменными.



