Окружность вписана в многоугольник, когда все вершины этого многоугольника лежат на окружности. Такая особенность геометрических фигур является важным свойством, которое возникает при определенных условиях. В этой статье мы рассмотрим определение и свойства многоугольника, в котором окружность вписана, а также рассмотрим несколько примеров, чтобы лучше понять эту концепцию.
Одно из основных свойств многоугольника, в котором окружность вписана, заключается в том, что центр окружности и центр многоугольника совпадают. То есть, если провести линию от центра окружности до какой-либо вершины многоугольника, она будет радиусом окружности. Кроме того, все радиусы окружности, проведенные к вершинам многоугольника, будут равны между собой.
Окружность, вписанная в многоугольник, также имеет связь с внешней окружностью многоугольника. Радиус внешней окружности многоугольника будет совпадать с радиусом вписанной окружности, а тангенциальные линии, проведенные от вершин многоугольника до вписанной окружности, будут проходить через точки касания внешней окружности с его сторонами.
Окружность вписана в многоугольник
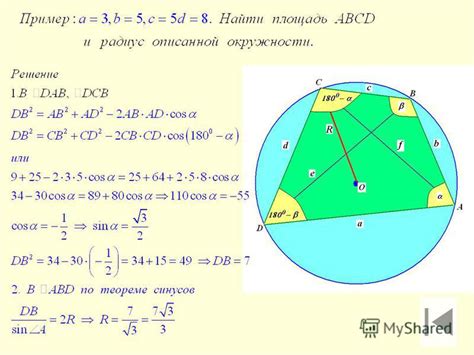
Свойства окружности, вписанной в многоугольник:
- Точка пересечения сторон многоугольника с окружностью является точкой касания.
- Линии, соединяющие вершины многоугольника с центром окружности, делят стороны многоугольника на равные отрезки.
- Сумма длин отрезков, соединяющих вершины многоугольника с центром окружности, равна периметру многоугольника.
Окружность вписана во многоугольник может быть найдена для многоугольников разного количества сторон: треугольника, четырехугольника, пятиугольника и так далее. Все эти случаи обладают вышеупомянутыми свойствами.
Окружность вписана в многоугольник находит применение в геометрических рассуждениях и вычислениях. Она помогает определить центр многоугольника, а также использовать впоследствии другие свойства и теоремы для нахождения площади многоугольника и его характеристик.
Определение и особенности

Важно отметить, что вписанная окружность также называется инкрустированной окружностью. Каждая точка касания между окружностью и многоугольником называется точкой касания или ортоцентрической точкой.
Многоугольник с вписанной окружностью имеет ряд особенностей:
- Сумма длин отрезков, проведенных от каждой вершины многоугольника до точки касания на окружности, равна полупериметру многоугольника.
- Сумма радиусов всех вписанных окружностей, вписанных в многоугольник, равна радиусу окружности, вписанной в многоугольник.
- Отношение площадей вписанного многоугольника и окружности, вписанной в него, стремится к отношению 1:π при увеличении числа сторон многоугольника.
Окружность, вписанная в многоугольник, играет важную роль в геометрии и имеет множество применений в различных областях, таких как архитектура, инженерное дело и математика.
Свойства вписанной окружности
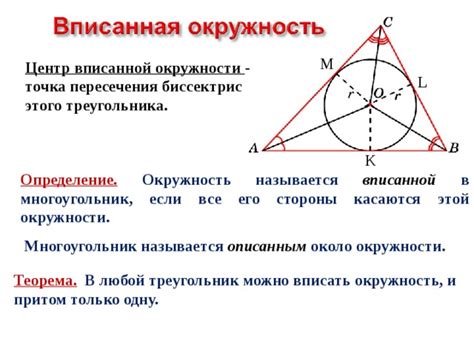
Вписанная окружность, или инкруг, это окружность, которая касается всех сторон многоугольника в его внутренних точках. Вписанная окружность имеет несколько особых свойств, которые она наследует от самого многоугольника:
| Свойство | Описание |
|---|---|
| Точка касания | Вписанная окружность касается каждой стороны многоугольника в ее внутренней точке, называемой точкой касания. |
| Радиус | Радиус вписанной окружности равен радиусу окружности, центр которой является центром многоугольника. |
| Тангенциальность | Линии, соединяющие вершины многоугольника с точками касания, называются радиусами. Они являются прямыми и касаются вписанной окружности. |
| Центр окружности | Центр вписанной окружности совпадает с центром многоугольника, который определяется точкой пересечения биссектрис. |
Свойства вписанной окружности являются важными при решении геометрических задач, так как они позволяют установить взаимосвязь между окружностями и многоугольниками. Также вписанная окружность имеет много применений в различных областях науки и техники.
Примеры многоугольников с вписанной окружностью
Равносторонний треугольник
Равносторонний треугольник - это треугольник, у которого все стороны имеют одинаковую длину. Окружность, вписанная в равносторонний треугольник, касается всех трех сторон в их точках пересечения. Это создает симметричную и гармоничную композицию.
Квадрат
Квадрат - это многоугольник с четырьмя равными сторонами и прямыми углами. Окружность, вписанная в квадрат, касается всех четырех сторон посередине и создает интересный геометрический паттерн.
Пятиугольник
Пятиугольник - это многоугольник с пятью сторонами. Окружность, вписанная в пятиугольник, касается каждой из пяти сторон в их точках пересечения. Вписанная окружность делит пятиугольник на более мелкие треугольники, создавая сложные геометрические связи.
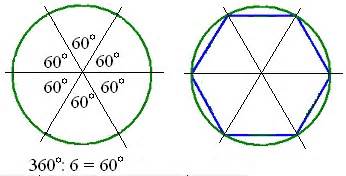
Шестиугольник
Шестиугольник - это многоугольник с шестью сторонами. Окружность, вписанная в шестиугольник, касается каждой из шести сторон в их точках пересечения. Расположение вершин шестиугольника вокруг вписанной окружности создает гармоничный и симметричный вид.
Это всего лишь несколько примеров многоугольников с вписанной окружностью. Вписанная окружность является важным элементом геометрии, используемым в различных областях, от математики до архитектуры.
Применение вписанной окружности

Вписанная окружность многоугольника имеет множество важных свойств и применений. Рассмотрим некоторые из них:
- Определение центра многоугольника:
- Определение радиуса окружности:
- Определение площади многоугольника:
- Улучшение точности приближения:
- Вычисление длин сторон многоугольника:
Центр вписанной окружности многоугольника совпадает с центром самого многоугольника. Это свойство можно использовать для определения центра многоугольника и его окружности.
Радиус вписанной окружности многоугольника можно вычислить с помощью формулы: радиус равен половине длины стороны многоугольника, деленной на тангенс половины центрального угла многоугольника.
Площадь многоугольника можно вычислить, зная радиус вписанной окружности и количество его сторон. Формула для расчета площади многоугольника: S = P * r / 2, где S - площадь, P - периметр многоугольника, r - радиус вписанной окружности.
Вписанная окружность может использоваться для улучшения точности приближения многоугольника к окружности. Чем больше сторон у многоугольника, тем ближе он будет приближаться к окружности.
Используя вписанную окружность, можно вычислить длины сторон многоугольника. Для этого достаточно измерить радиус вписанной окружности и умножить его на тангенс половины центрального угла многоугольника.
Вписанная окружность является важным инструментом для изучения свойств и характеристик многоугольников. Она помогает в решении различных геометрических задач, и ее применение широко используется в математике, физике и других научных областях.



