Параллелограмм – это одна из наиболее интересных и изучаемых в геометрии фигур. Он относится к некоторому классу четырехугольников и имеет множество уникальных свойств. Параллелограмм может быть описан как выпуклый четырехугольник, у которого противоположные стороны параллельны и равны между собой. Это простое определение, но параллелограмм обладает гораздо большим количеством особенностей, которые его отличают от других фигур.
Главное свойство параллелограмма заключается в том, что его противоположные стороны всегда параллельны. Это означает, что если провести две прямые, которые попарно параллельны сторонам параллелограмма, они будут пересекать друг друга в точке, делящей их пополам.
Другим важным свойством параллелограмма является то, что его противоположные углы равны. Если обозначить эти углы как А и С, а остальные два угла как В и D, то мы можем сказать, что А = С и В = D. Это следует из построения фигуры и ее геометрических свойств.
Определение и свойства параллелограмма

У параллелограмма есть несколько важных свойств:
- Противоположные стороны параллельны: это означает, что каждая сторона параллелограмма находится на одной линии с противоположной стороной и никогда не пересекает ее.
- Противоположные стороны равны: все противоположные стороны параллелограмма имеют одинаковую длину. Это означает, что сторона АВ равна стороне CD, а сторона BC равна стороне DA.
- Углы при основании равны: основанием параллелограмма являются противоположные стороны AB и CD. Углы, образованные этими сторонами с остальными сторонами параллелограмма, имеют одинаковую величину.
- Сумма углов параллелограмма равна 360 градусов: это означает, что если сложить все углы параллелограмма, получится 360 градусов. Например, если один угол параллелограмма равен 90 градусов, то каждый из остальных углов будет равен 90 градусов, чтобы в сумме получилось 360 градусов.
- Диагонали параллелограмма делятся пополам: это означает, что диагонали AC и BD параллелограмма делятся пополам и пересекаются в точке O, которая является центром симметрии параллелограмма.
Эти свойства позволяют определить и распознать параллелограмм и установить его основные характеристики.
Углы параллелограмма

В параллелограмме противоположные углы равны между собой. Это значит, что угол A равен углу C, а угол B равен углу D. Это следует из того факта, что параллельные стороны пересекаются под одинаковыми углами.
Кроме того, сумма углов в параллелограмме равна 360 градусов. Если мы обозначим углы параллелограмма как A, B, C и D, то A + B + C + D = 360°.
Для вычисления отдельных углов в параллелограмме можно использовать знание о том, что дополнительные углы равны. Например, угол A и угол D являются дополнительными, поэтому их сумма равна 180 градусов. Аналогично, угол B и угол C также дополнительные и равны 180 градусам.
Изучение углов параллелограмма позволяет лучше понять его геометрические свойства и применять эти знания для решения различных задач и задач в области математики и физики.
Стороны параллелограмма
1. Боковые стороны - это две параллельные стороны параллелограмма, которые соединяют две противоположные вершины. Боковые стороны равны по длине, так как параллелограмм - это равнобедренный четырехугольник.
2. Верхняя сторона - это сторона параллелограмма, которая соединяет две противоположные вершины и лежит в верхней части фигуры. Она параллельна нижней стороне и имеет равную длину с ней.
3. Нижняя сторона - это сторона параллелограмма, которая соединяет две противоположные вершины и лежит в нижней части фигуры. Она параллельна верхней стороне и имеет равную длину с ней.
Итак, у параллелограмма есть две боковые стороны, верхняя и нижняя стороны, которые параллельны и равны по длине. Зная любую из сторон, можно легко найти все остальные стороны параллелограмма.
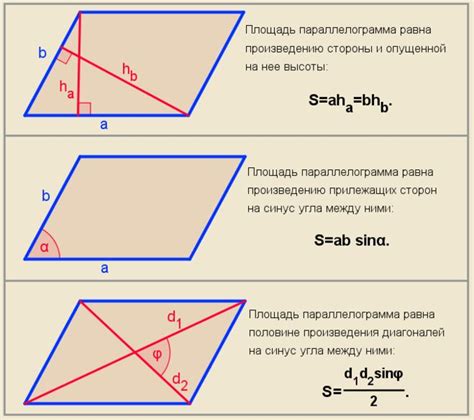
Площадь параллелограмма
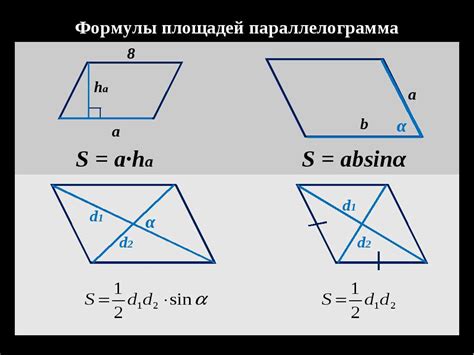
Также площадь параллелограмма можно найти, зная длины двух его сторон и угол между ними. Формула для расчета площади параллелограмма по этим данным S = a * b * sin(α), где a и b - длины сторон, α - угол между ними.
Если известны длины всех сторон параллелограмма, можно воспользоваться формулой Герона для нахождения площади. Сначала найдем полупериметр параллелограмма p = (a + b + c + d) / 2, затем расчитаем площадь по формуле S = sqrt((p - a) * (p - b) * (p - c) * (p - d)), где a, b, c, d - длины сторон параллелограмма.
Зная координаты вершин параллелограмма в декартовой системе координат, площадь можно найти по формуле Гаусса S = (1/2) * |x1y2 + x2y3 + x3y4 + x4y1 - x2y1 - x3y2 - x4y3 - x1y4|, где xi и yi - координаты вершины параллелограмма.
Высота параллелограмма

Для нахождения высоты параллелограмма можно воспользоваться следующей формулой:
h = (2 * Площадь параллелограмма) / длина основания
Где:
h - высота параллелограмма;
Площадь параллелограмма - произведение длин стороны параллелограмма на длину высоты, опущенной на эту сторону;
длина основания - длина стороны, к которой опущена высота.
Высота параллелограмма позволяет найти его площадь, которая определяется как произведение длины любой стороны параллелограмма на длину высоты, опущенной на эту сторону.
Таким образом, зная высоту параллелограмма, можно рассчитать его площадь и использовать эту информацию при решении различных задач и построении графиков.
Диагонали параллелограмма
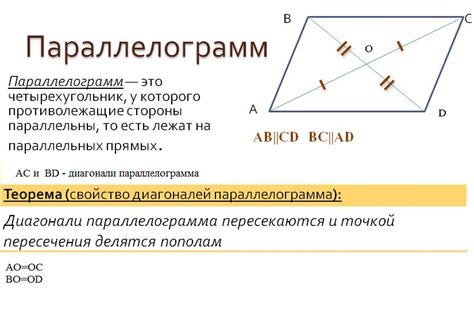
У параллелограмма есть две диагонали - главная и второстепенная. Главная диагональ - это отрезок, соединяющий противоположные вершины параллелограмма. Главная диагональ делит параллелограмм на два равных треугольника.
Второстепенная диагональ - это отрезок, соединяющий другие две противоположные вершины параллелограмма. Второстепенная диагональ также делит параллелограмм на два равных треугольника.
Свойства диагоналей параллелограмма:
| Главная диагональ | Второстепенная диагональ |
| 1. Длина главной диагонали равна длине второстепенной диагонали. | 1. Длина главной диагонали равна длине второстепенной диагонали. |
| 2. Главная диагональ делит параллелограмм на два равных треугольника. | 2. Второстепенная диагональ делит параллелограмм на два равных треугольника. |
| 3. Главная диагональ является осью симметрии параллелограмма. | 3. Второстепенная диагональ является осью симметрии параллелограмма. |
Диагонали параллелограмма также могут использоваться для вычисления площади и других характеристик фигуры.
Примеры параллелограммов в природе

1. Цветущий растительный стебель
Когда наблюдаемая часть стебля растения вытянута вертикально, а листья растут попарно по противоположным сторонам стебля, форма стебля и листьев может быть приближена к параллелограмму. Например, у некоторых видов бамбука или кустарников встречаются параллелограммальные листья.
2. Узоры на песке или гравии
Природные факторы, такие как вода, ветер или паводки, могут создавать параллелограммальные узоры на песке или гравии. Например, приливно-отливные процессы на морском или океанском побережье могут оставлять на песчаном пляже параллельные следы от прибоя.
3. Кристаллические формы
Многие кристаллы обладают параллелограммальной формой, которая связана с регулярной структурой и симметрией атомов или молекул в кристаллической решетке. Примерами таких кристаллов могут быть кварц, графит или соль.
Это только несколько примеров параллелограммов, которые можно обнаружить в природе. Изучение геометрии и ее применение в реальном мире позволяют увидеть, как многообразна и универсальна эта наука.



