Определение принадлежности точки закрашенной области - это задача из области компьютерной геометрии, которая заключается в определении, принадлежит ли заданная точка закрашенной области на плоскости или нет. Эта задача имеет широкий спектр применений, начиная от создания графических приложений и компьютерных игр, и заканчивая анализом изображений и обработкой географических данных.
Существует несколько методов для определения принадлежности точки закрашенной области, каждый из которых имеет свои преимущества и ограничения. Одним из таких методов является алгоритм трассировки лучей, который строит луч из заданной точки и подсчитывает количество пересечений луча с границами закрашенной области. Если количество пересечений нечетное, то точка находится внутри закрашенной области, в противном случае - снаружи.
Другим методом является алгоритм заполнения с затравкой, который заключается в выборе стартовой точки внутри закрашенной области и последующем заполнении области, с помощью проверки соседних пикселей на совпадение с цветом границы. Если соседний пиксель совпадает, то текущий пиксель принадлежит закрашенной области, в противном случае - считается снаружи.
В данной статье будут рассмотрены эти и другие методы определения принадлежности точки закрашенной области, а также приведены примеры их использования в различных задачах.
Метод ближайшей точки и алгоритм явного разбиения на треугольники

Алгоритм явного разбиения на треугольники заключается в том, что исходная область разбивается на треугольники с помощью специальных алгоритмов. Затем производится проверка каждого треугольника на принадлежность точки к нему. Если точка принадлежит хотя бы одному треугольнику, то считается, что она принадлежит закрашенной области. В противном случае, точка считается не принадлежащей области.
Алгоритм растровой обработки и принцип граничного пересечения
Алгоритм растровой обработки представляет собой метод определения принадлежности точки закрашенной области на растровом изображении. Этот алгоритм имеет широкое применение в компьютерной графике, географических системах и визуализации данных.
Одним из ключевых понятий при использовании алгоритма растровой обработки является принцип граничного пересечения. Суть этого принципа заключается в том, что границы областей на растровом изображении определяются пересечением луча от исследуемой точки с границами областей.
Процесс определения принадлежности точки закрашенной области, используя алгоритм растровой обработки и принцип граничного пересечения, можно разделить на следующие шаги:
- Выбрать исследуемую точку на растровом изображении.
- Провести луч от исследуемой точки в направлении, отличном от оси координат.
- Определить количество пересечений луча с границами областей на изображении.
- Если количество пересечений нечетное, то точка принадлежит закрашенной области, иначе – точка не принадлежит области.
Принцип граничного пересечения позволяет достаточно эффективно определить принадлежность точки закрашенной области без необходимости проверки каждого пикселя растрового изображения. За счет использования луча и пересечения с границами областей, данный алгоритм может быть применен для работы с различными формами областей.
Примером применения алгоритма растровой обработки и принципа граничного пересечения может быть определение принадлежности точки внутренней части многоугольника на растровом изображении. В этом случае, границы области представляют собой границы многоугольника, а луч, проведенный из исследуемой точки, пересекает эти границы. Таким образом, можно определить, находится ли точка внутри или снаружи многоугольника.
Корректное определение границ области без самопересечений
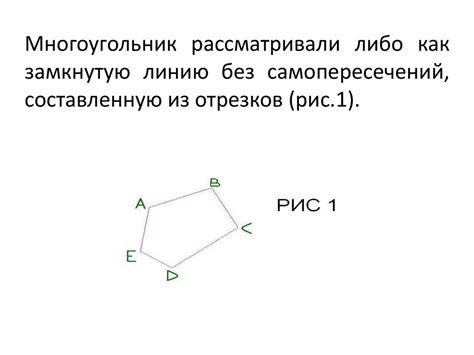
Определение принадлежности точки закрашенной области может быть сложной задачей, особенно в случае, когда область имеет сложную форму или содержит самопересечения.
Для корректного определения границ области без самопересечений можно использовать различные методы.
- Метод пересечения лучей: Данный метод заключается в том, чтобы нарисовать луч, направленный от рассматриваемой точки в произвольном направлении и посчитать количество пересечений этого луча с границей области. Если количество пересечений четное, то точка не принадлежит области, а если нечетное - точка принадлежит области. Этот метод может быть применен для простых выпуклых областей без самопересечений.
- Метод триангуляции: В этом методе область разбивается на небольшие треугольники, затем определяется, в каком треугольнике находится рассматриваемая точка. Путем проверки положения точки относительно сторон и углов треугольников можно определить, принадлежит ли точка закрашенной области или нет.
- Метод контуров: Этот метод основывается на использовании алгоритма, который находит все контуры границы области и строит полигоны вокруг каждого контура. Затем точка проверяется на принадлежность каждому полигону. Если точка принадлежит хотя бы одному полигону, то она принадлежит области, иначе - нет.
При выборе метода определения принадлежности точки закрашенной области необходимо учитывать особенности задачи, форму области и ее сложность, а также требуемую точность определения.
Преимущества и недостатки каждого метода и их применение

Существует несколько методов определения принадлежности точки закрашенной области на плоскости. Каждый из этих методов имеет свои преимущества и недостатки, а также различные области применения.
Метод геометрической алгебры
Преимущества:
- Простота и понятность алгоритма
- Высокая скорость выполнения
Недостатки:
- Неэффективность при работе с комплексными структурами
- Ограниченность в применении для сложных форм областей
Применение:
Метод геометрической алгебры широко используется для простых геометрических фигур, таких как круги, прямоугольники и треугольники.
Метод растровых изображений
Преимущества:
- Позволяет работать с изображениями любой сложности
- Гибкость и точность получаемого результата
Недостатки:
- Высокая вычислительная сложность
- Требует большого объема памяти
Применение:
Метод растровых изображений часто используется в компьютерном зрении и передаче видео, где требуется обработка и анализ большого количества пикселей.
Метод геометрического анализа
Преимущества:
- Подходит для сложных форм областей
- Высокая точность результата
Недостатки:
- Сложность формализации алгоритма
- Высокая вычислительная сложность для больших объемов данных
Применение:
Метод геометрического анализа применяется в задачах компьютерного моделирования, анализа геометрических форм и имеет широкое применение в машинном зрении.
Примеры реализации определения принадлежности в различных языках программирования
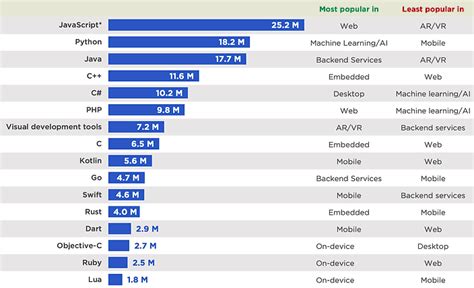
Определение принадлежности точки закрашенной области может быть реализовано с использованием различных языков программирования. Ниже приведены примеры реализации данной задачи на нескольких популярных языках.
- JavaScript:
function isPointInArea(x, y) {
// Проверка условия принадлежности точки
if (x >= 0 && x <= 10 && y >= 0 && y <= 10) {
return true;
} else {
return false;
}
}
// Пример вызова функции
console.log(isPointInArea(5, 5)); // Вернет true
console.log(isPointInArea(15, 5)); // Вернет false
def is_point_in_area(x, y):
# Проверка условия принадлежности точки
if 0 <= x <= 10 and 0 <= y <= 10:
return True
else:
return False
# Пример вызова функции
print(is_point_in_area(5, 5)) # Вернет True
print(is_point_in_area(15, 5)) # Вернет False
public static boolean isPointInArea(int x, int y) {
// Проверка условия принадлежности точки
if (x >= 0 && x <= 10 && y >= 0 && y <= 10) {
return true;
} else {
return false;
}
}
// Пример вызова функции
System.out.println(isPointInArea(5, 5)); // Вернет true
System.out.println(isPointInArea(15, 5)); // Вернет false
Приведенные примеры демонстрируют, как можно реализовать определение принадлежности точки закрашенной области на различных языках программирования. При этом принцип работы одинаков для всех языков: проверка условия принадлежности координат точки заданному диапазону.



