Логика – это дисциплина, которая изучает правила и принципы верного мышления. Она помогает нам анализировать и организовывать наши мысли, а также строить аргументы и доказательства. Важно понимать, что логика является неотъемлемой частью нашей повседневной жизни, ведь мы ежедневно сталкиваемся с различными логическими задачами и проблемами.
Одним из ключевых понятий в логике является понятие истинности. Логическое выражение может быть истинным или ложным. Например, выражение "2 + 2 = 4" является истинным, в то время как выражение "2 + 2 = 5" является ложным. Используя правила логики, мы можем анализировать и проверять истинность различных высказываний.
Принципы логики помогают нам строить логически правильные аргументы. Один из основных принципов логики – это принцип непротиворечивости. Согласно этому принципу, нельзя одновременно утверждать и отрицать одно и то же высказывание. Например, нельзя сказать, что "сегодня идет дождь" и "сегодня не идет дождь" одновременно. Этот принцип позволяет нам избегать противоречий в рассуждениях и аргументациях.
Логика: определение и значение

Одним из ключевых понятий в логике является понятие "истины". Истина - это такое состояние знания, когда оно соответствует действительности. В логике истина выражается логическими высказываниями, которые могут быть либо истинными, либо ложными.
Еще одним понятием, играющим важную роль в логике, является понятие "противоречия". Противоречие возникает, когда два логических высказывания противоречат друг другу, то есть одновременно не могут быть истинными.
Тогда и только тогда: ключевое понятие логики

Когда говорят о "тогда и только тогда", подразумевается, что для того, чтобы что-то произошло или было верным, должны быть выполнены определенные предпосылки. Это является основным принципом логического мышления. Используя это понятие, мы можем логически анализировать и оценивать ситуации, а также принимать информированные решения.
Примером использования "тогда и только тогда" является использование условных утверждений в математике и программировании. Например, "x равен 5 тогда и только тогда, когда x + 2 равно 7". В этом примере, предпосылкой для истинности первого утверждения является то, что сумма x + 2 равна 7.
Ключевое понятие "тогда и только тогда" также используется в логических операторах, таких как "и", "или" и "не". Например, "A и B истинны тогда и только тогда, когда и A, и B истинны". Эта логическая формула означает, что для того, чтобы утверждение А и утверждение В были истинны, оба утверждения должны быть истинны.
Ключевые принципы логики
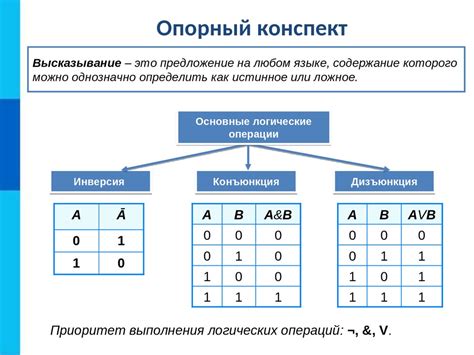
Существует несколько ключевых принципов логики, которые помогают понять основы этой науки. Они являются основой для построения законных доводов и корректных рассуждений. Вот некоторые из них:
- Принцип идентичности: то, что истинно, истинно. Если утверждение А равно утверждению А, то они тождественны.
- Принцип противоречия: нельзя одновременно утверждать и отрицать одно и то же. Если утверждение А противоречит утверждению В, то они не могут быть оба истинными.
- Принцип исключённого третьего: утверждение либо истинно, либо ложно. Утверждения не могут находиться в промежуточном состоянии.
- Принцип достаточного основания: каждое утверждение должно иметь основание или доказательство. Если утверждение не имеет оправдания, то оно не может быть считаться логически обоснованным.
- Принцип эквивалентности замены: утверждения, эквивалентные друг другу, могут заменять друг друга в любом рассуждении или доказательстве.
Основные понятия логики

Одним из основных понятий логики является понятие «истина». В логике истина определена как утверждение, которое соответствует действительности. Существуют различные подходы к определению истины, включая корреспондентный, когерентный и прагматический подходы.
Другим важным понятием в логике является «логическая связь». Логическая связь указывает на отношение между двумя или более утверждениями. Основные логические связи включают «и», «или», «не», «если-то» и «только если».
Еще одним ключевым понятием логики является «логическое следование». Логическое следование указывает на отношение между двумя утверждениями, при котором первое утверждение (предпосылка) гарантирует истинность второго утверждения (следствие).



