Бесконечность – это понятие, которое всегда вызывает у нас интерес и удивление. Оно глубоко пронизывает нашу жизнь и философские рассуждения. Бесконечность обладает свойствами, которые сложно понять и описать. В математике бесконечность не является исключением. Существует такое явление, как бесконечность функций, когда нет предела.
Функции в математике – это своего рода "машины", которые преобразуют одно число в другое. Они используются для описания различных явлений и процессов. Часто функции имеют определенные пределы, когда значение функции стремится к определенной точке приближения.
Однако, существуют функции, которые не имеют предела. Они могут бесконечно "растягиваться" или "сжиматься" на числовой оси, не приближаясь к какому-либо конкретному значению. Это столь абстрактное и сложное явление, что его понимание требует особого ума и математической интуиции.
Что такое бесконечность функций?

Когда функция не имеет предела, это означает, что она не стремится к какому-либо определенному значению или неограниченно растет/убывает с увеличением значения переменной.
Для таких функций нельзя однозначно определить, как они будут вести себя в бесконечности. На графике они могут между собой переплетаться, иметь различные пики и впадины и в целом проявлять непредсказуемое поведение.
Такие функции могут встречаться в различных областях математики и физики, особенно в тех случаях, когда моделируются сложные и нелинейные системы. Они могут быть использованы для описания частиц, звезд, расстояний и т.д.
| Пример 1: | Функция f(x) = sin(x)/x |
|---|---|
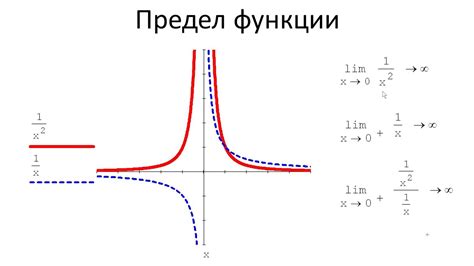
| Пример 2: | Функция f(x) = 1/x |
В этих случаях, при x -> бесконечности, функции не имеют предела и их поведение в бесконечности будет различным.
"Бесконечность функций" - это понятие, которое помогает нам понять сложное и непредсказуемое поведение функций в бесконечности и исследовать их свойства с помощью математических методов и анализа.
Бесконечность и пределы

Предел функции – это концепция, которая описывает поведение функции при стремлении аргумента к определенному значению. Если предел функции существует и равен бесконечности, то говорят, что функция имеет предел в бесконечности.
Понятие предела позволяет описывать сложное поведение функций в окрестности особых точек или на бесконечности. Благодаря концепции предела, мы можем формально разграничивать различные виды бесконечностей и анализировать их характеристики.
Бесконечность и пределы широко используются в различных областях математики, физики и других наук для решения сложных задач и построения моделей. Понимание концепции предела и бесконечности является необходимым навыком для математического анализа и дальнейшего изучения функций.
Причины отсутствия предела

Существует несколько причин, по которым функция может не иметь предела:
1. Рост функции до бесконечности Если функция растет неограниченно, то она не будет иметь предела. Например, при функции f(x) = x, при x, стремящемся к бесконечности, значение функции также будет бесконечно расти. |
2. Периодическая функция Если функция периодическая, то ее значения будут постоянно колебаться между определенными границами. Такие функции также не имеют предела, так как значения не стремятся к конкретному числу. |
3. Дублирование значений Если функция имеет дублирующиеся значения, то она не может иметь предела. Например, функция f(x) = sin(x) имеет значения от -1 до 1 и они повторяются бесконечное количество раз. |
4. Несобственный интеграл Функция может не иметь предела, если ее несобственный интеграл расходится. Несобственные интегралы могут возникать, когда функция имеет особенности, такие как разрывы или вертикальные асимптоты. |
Важно помнить, что отсутствие предела не означает, что функция не имеет значения. Она может иметь значения в определенных точках, но эти значения не подчиняются никакому конкретному закону и не сходятся к определенному числу.
Бесконечные функции в математическом анализе

Бесконечная функция означает, что значений функции может быть неограниченное количество или что функция может стремиться к бесконечности в определенных точках.
Одним из примеров бесконечной функции является функция f(x) = 1/x. В этом случае, если x стремится к нулю, значением функции будет бесконечность. Это известно как вертикальная асимптота.
Также, существуют функции, которые могут иметь бесконечное количество значений. К примеру, функция g(x) = x^2, в этом случае, при увеличении значения x, значений функции также будет бесконечно много.
Для изучения бесконечных функций, в математическом анализе используются понятия предела и бесконечно больших и малых значений. Границы функции и ее поведение в бесконечности являются ключевыми аспектами при анализе таких функций.
Изучение бесконечных функций имеет множество применений в физике, экономике, и других областях науки. Например, они могут быть использованы для моделирования процессов, которые имеют тенденцию к бесконечности, таких как экспоненциальный рост или угасание.
Таким образом, бесконечные функции представляют важную часть математического анализа, и изучение их свойств и поведения позволяет более глубоко понять различные аспекты функций и их применение в реальном мире.
Примеры бесконечных функций

Существует множество функций, которые не имеют предела и продолжают увеличиваться или уменьшаться бесконечно. Вот несколько примеров:
1. Функция f(x) = x^2
Приближаясь к положительной или отрицательной бесконечности, значение функции увеличивается бесконечно. При этом, функция не имеет конечного предела.
2. Функция f(x) = 1/x
Приближаясь к нулю справа или слева, функция увеличивается или уменьшается бесконечно. Она не имеет предела в нуле.
3. Функция f(x) = sin(x)
Функция синуса колеблется между значениями -1 и 1 вечно и не имеет предела.
Это лишь несколько примеров из множества бесконечных функций. Их изучение в математике помогает понять различные аспекты бесконечности и анализировать поведение функций в различных точках.
Практическое применение бесконечных функций
Бесконечные функции, такие как рекурсивные функции и функции с бесконечным числом аргументов, могут быть полезны во многих практических сценариях. Они позволяют нам работать с бесконечными последовательностями и представлять комплексные математические концепции.
Одним из практического применения бесконечных функций является вычисление бесконечных последовательностей. Например, ряд Тейлора является бесконечной последовательностью, которая сходится к определенному значению. Мы можем использовать рекурсивные функции для вычисления этого ряда и получения приближенного значения функции в заданной точке.
Еще одним примером практического применения бесконечных функций является моделирование физических процессов. Например, волновая функция в квантовой механике является бесконечной функцией, которая описывает состояние частицы. Мы можем использовать функции с бесконечным числом аргументов для представления этой волновой функции и анализировать свойства частицы.
Также бесконечные функции могут быть полезны при моделировании и аппроксимации реальных данных. Например, при анализе временных рядов или прогнозировании будущих значений мы можем использовать бесконечные функции для аппроксимации и предсказания значений в бесконечном горизонте времени.
| Применение | Пример |
|---|---|
| Ряды Тейлора | exp(x) = 1 + x + x^2/2! + x^3/3! + ... |
| Квантовая механика | Волновая функция электрона |
| Анализ временных рядов | Аппроксимация тренда данных |
Бесконечные функции имеют много практических применений и позволяют нам работать с сложными математическими концепциями. Они помогают нам моделировать физические процессы, анализировать данные и предсказывать значения в будущем.
Бесконечные функции в физике
В физике мы часто сталкиваемся с бесконечными функциями, которые описывают различные физические явления. Бесконечные функции широко применяются для моделирования свойств материалов, движения частиц, электромагнитных полей и многих других физических процессов.
Например, в оптике мы можем использовать бесконечные функции для описания распределения интенсивности света в пространстве. Такие функции могут быть особенно полезны в случаях, когда интенсивность света в определенных точках пространства стремится к бесконечности или к нулю.
В классической механике также могут возникать бесконечные функции при описании движения материальных объектов. Например, в случае свободного падения тела под воздействием гравитационной силы, функция, описывающая положение тела от времени, может иметь предел, равный бесконечности.
Еще одним примером бесконечных функций в физике являются функции, описывающие электромагнитные поля. В случае точечного заряда электрическое поле в некоторых точках пространства может иметь бесконечное значение. Такие функции помогают нам понять и предсказать электромагнитные взаимодействия между зарядами.
Таким образом, бесконечные функции играют важную роль в физике. Они позволяют нам описывать и понимать различные физические явления, включая распределение света, движение материалов и электромагнитные поля. Без понимания и использования бесконечных функций, наше представление о физическом мире было бы значительно ограничено.



