Наука теории графов является одной из важнейших областей математики и информатики. Она исследует свойства и структуру графов, которые представляют собой абстрактные модели связей между объектами. Но как и когда возникла эта наука?
История теории графов уходит своими корнями в XVIII век. В 1736 году швейцарский математик и физик Леонард Эйлер в своей знаменитой работе "Задача о семи мостах Кёнигсберга" предложил новый подход к решению проблемы. Эйлер сформулировал основные понятия теории графов, такие как ребра, вершины и циклы, и разработал методы их анализа.
Однако, настоящий прорыв в развитии теории графов произошел только в XX веке. В 1936 году венгерский математик Деньеш Кёниг обнаружил общую теорему о полных графах, которая с течением времени стала одной из основных теорем этой науки. В дальнейшем Кёниг и другие математики продолжали работать над развитием теории графов, создавая новые методы и алгоритмы, которые нашли широкое применение в различных областях науки и техники.
Сегодня теория графов активно развивается и привлекает внимание учёных со всего мира. Её результаты используются при решении множества задач в таких областях, как компьютерные науки, транспортное планирование, социология и даже биология. Становится все очевиднее, что наука теории графов будет продолжать развиваться и находить новые применения в будущем.
Возникновение науки теории графов

Наука теории графов появилась в середине XIX века благодаря работам швейцарского математика Леонарда Эйлера. В своей статье "Задача семи кёнигсбергских мостов" он предложил новый математический подход к изучению сетей связей.
Основываясь на географической карте города Кёнигсберг с речным проливом и семью мостами, Эйлер установил, что можно представить город в виде узлов и связей между ними. Так он первым открыл путь к абстрактному изучению объектов их связей без ссылки на конкретные материальные предметы.
Эйлер сформулировал основные понятия и правила теории графов, такие как граф, вершина, ребро и цикл. Он разработал математический аппарат для анализа графов и доказал теорему о связности.
Интересно отметить, что научное использование графов началось задолго до появления компьютеров и современной информационной технологии. Теория графов оказалась универсальным инструментом для моделирования и решения разных задач в самых различных областях знания.
В настоящее время исследования в области теории графов активно ведутся, и это направление математики и информатики стало одной из важнейших областей прикладных наук.
Истоки создания науки

История развития науки теории графов уходит своими корнями в XVIII век. Однако, все началось не с теории графов, а с задачи о Кёнигсбергских мостах.
В 1736 году прусский математик Леонард Эйлер решил известную задачу в городе Кёнигсберге: можно ли пройти по каждому из семи мостов города только один раз? Эйлер сформировал граф, где мосты представлены ребрами, а земли и реки - вершинами. Он доказал, что для того, чтобы пройти по каждому мосту всего один раз, необходимо, чтобы все вершины графа имели четную степень. В противном случае это невозможно.
Открытие Эйлера насчитывает более двух столетий, и с тех пор теория графов развивалась параллельно с развитием математики и информатики.
- В XIX веке Иоганн Вольфганг Гёсольд начал изучать графы в контексте комбинаторики и теории чисел. Он разработал понятие "эйлерова графа", где все вершины имеют четную степень, и "гамильтонова графа", где существует цикл, посещающий каждую вершину ровно один раз.
- В XX веке графовые структуры стали активно использоваться в компьютерных науках. Программисты и математики применяли теорию графов для решения задач связности и оптимизации.
- В 1956 году Луи Кашуалего и Томаса Кормена опубликовали книгу "Введение в алгоритмы", где теория графов появляется в качестве ключевой темы. Это стало одним из важнейших этапов в развитии науки теории графов, она стала важной частью компьютерных наук и информатики.
Теория графов применяется в самых разных областях, включая сетевую связь, социальные исследования, логистику, транспорт и даже биологию. Получив статус науки, теория графов продолжает активно развиваться и находить новые применения в современном мире.
Пионеры теории графов
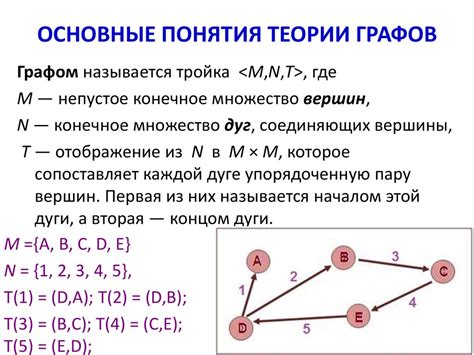
Одним из первых исследователей, которые внесли значительный вклад в развитие теории графов, был Леонард Эйлер. В 1735 году он решил знаменитую задачу о Кёнигсбергских мостах, которая привела к созданию первой теоремы о графах. Эйлер представил город Кёнигсберг и его семь мостов в виде графа, где земля обозначалась точками (вершинами графа), а мосты – линиями (ребрами графа). Чтобы пройти по каждому мосту всего один раз и вернуться в точку отправления, число возможных путей должно быть четным. Эта теорема в дальнейшем стала известна как Теорема Эйлера.
Другим выдающимся математиком, внесшим огромный вклад в теорию графов, был Артур Кэли. В 1857 году Кэли разработал понятие графа и применил его в анализе групповых структур. Его работа стала основанной для дальнейшего развития теории графов и применения ее в различных областях, таких как транспорт, телекоммуникации, биология и социология.
Важным вкладом в развитие теории графов было также исследование Клири Харшалла. В своей работе 1852 года он впервые ввел понятие связности в графах и доказал основные свойства связных графов. Эти исследования положили основу для развития множества алгоритмов и методов анализа графов, которые находят широкое применение в настоящее время.
Таким образом, благодаря работе пионеров теории графов, таких как Эйлер, Кэли и Харшалл, наука получила мощный инструмент для анализа сложных структур и взаимодействий в различных областях знания.
Развитие теории графов в настоящее время
Наука теории графов продолжает активно развиваться в настоящее время. В связи с развитием компьютерных технологий и возросшим интересом к анализу сложных систем, теория графов становится все более востребованной и находит широкое применение в различных областях науки и техники.
Современные исследования в области теории графов направлены на разработку новых методов анализа и алгоритмов для работы с графовыми структурами. Одним из основных направлений развития является изучение сложности задач, связанных с графами, и разработка эффективных алгоритмов для их решения.
Также активно исследуются графы большой размерности, например, графы социальных сетей или сетей передачи данных. Важная задача заключается в разработке методов и алгоритмов для анализа и визуализации больших графов, которые позволят эффективно извлекать информацию из таких сложных структур.
В настоящее время теория графов применяется в различных областях, включая информатику, математику, физику, экономику, социологию и многие другие. Она находит применение в анализе сетей связей, моделировании транспортных систем, оптимизации процессов и принятии решений.
| Область применения | Пример |
|---|---|
| Информатика | Анализ социальных сетей |
| Математика | Теория графов |
| Физика | Моделирование транспортных систем |
| Экономика | Оптимизация процессов |
| Социология | Анализ социальных сетей |
Развитие технологий и интерес к исследованию сложных систем позволяют предполагать, что теория графов будет продолжать развиваться и находить все новые применения в научных и практических областях.



