Непараметрическая статистика – это раздел математической статистики, который не предполагает предварительных предположений о распределении данных или параметрах модели. В отличие от параметрической статистики, непараметрические методы могут быть применены в ситуациях, когда данные не подчиняются стандартным распределениям или когда о распределении данных ничего не известно.
Условия применения непараметрических методов статистики определяются главным образом свойствами исследуемых данных и задачей, которую необходимо решить. Непараметрические методы широко используются в различных областях, включая медицину, экономику, психологию и социологию. Они позволяют получать более надежные результаты в случае, когда нет возможности использовать параметрические методы или когда параметрические методы не дают адекватных результатов.
Основными условиями, при которых может потребоваться применение непараметрических методов статистики, являются: небольшой объем выборки, наличие выбросов, нарушение предположений о нормальности распределения данных, отсутствие линейных зависимостей между переменными, наличие неупорядоченных или ранговых переменных. Непараметрические методы также применяются, если исследуемая задача не требует оценки конкретных параметров или построения математических моделей.
Понятие непараметрической статистики и ее роль

Роль непараметрической статистики заключается в том, чтобы предоставить методы анализа данных, когда классические методы неприменимы. Она помогает исследователям извлекать информацию из данных, не зависимо от формы распределения.
Непараметрические методы статистики широко применяются в различных областях, таких как медицина, экономика, психология и т.д. Они часто используются для сравнения групп, оценки эффективности лечения, проверки гипотезы о различии между наборами данных и многих других задач.
Основным преимуществом непараметрических методов является их независимость от предположений о распределении данных. Это делает их более гибкими и универсальными для различных типов данных и сценариев. Кроме того, они могут быть применены к небольшим выборкам и обеспечивают более консервативные (без предположений) оценки.
| Преимущества | Недостатки |
|---|---|
| Независимость от предположений о распределении данных | Могут требоваться большие выборки |
| Универсальность и гибкость | Могут быть менее мощными при выполнении предположений |
| Применимость к различным типам данных | Могут быть менее эффективными |
Преимущества использования непараметрических методов

2. Работа с категориальными и порядковыми данными. Непараметрические методы широко используются для анализа категориальных и порядковых данных, которые не могут быть обработаны с помощью классических параметрических методов. Это, например, дает возможность анализировать результаты опросов или мнений людей.
4. Возможность применения с малыми выборками. В отличие от некоторых параметрических методов, непараметрические методы могут быть применены для анализа данных с малыми выборками. Они не требуют большого объема данных для получения статистически значимых результатов.
5. Богатый набор методов. Непараметрическая статистика предлагает множество методов и тестов для анализа различных типов данных и задач. Они позволяют решать широкий спектр статистических задач без необходимости предполагать распределение данных.
6. Безпараметрический подход к анализу. Непараметрические методы статистики предлагают безпараметрический подход к анализу данных, что означает, что они не требуют знания или задания каких-либо параметров распределения. Это делает их более гибкими и универсальными в использовании.
Ограничения и условия применения непараметрических методов

Однако, условия применения непараметрических методов имеют свои ограничения:
| Ограничение | Описание |
|---|---|
| Независимость | Непараметрические методы требуют, чтобы наблюдения были независимыми. Если данные содержат зависимости или взаимосвязи между наблюдениями, непараметрические методы могут давать неправильные или неадекватные результаты. |
| Размер выборки | Непараметрические методы не всегда могут быть эффективны при малых размерах выборки. В таких случаях может потребоваться использование альтернативных методов анализа данных. |
| Независимость выборок | Если данные разделены на независимые группы или выборки, непараметрические методы могут быть ограничены в своей способности анализировать эффекты и взаимосвязи между группами. |
| Нормальность распределения | Непараметрические методы не требуют нормальности распределения данных, однако, если данные все же подчиняются нормальному распределению, то использование параметрических методов могло бы быть более эффективным. |
Помимо этих ограничений, следует учитывать и другие факторы, такие как тип и цель исследования, доступность данных, а также предпочтения и опыт исследователя. Применение непараметрических методов статистики требует внимательного анализа и оценки всех факторов, чтобы выбрать наиболее подходящий подход для анализа данных.
Выбор критерия при использовании непараметрических методов
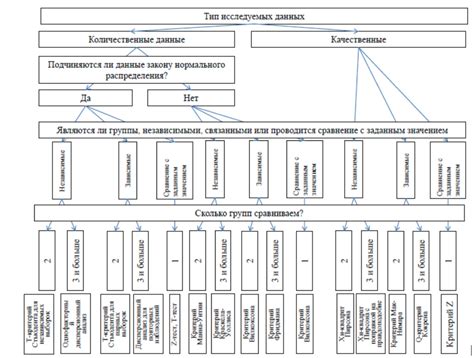
Одним из ключевых критериев, используемых в непараметрической статистике, является критерий Манна-Уитни, или U-тест. Он используется для сравнения двух независимых выборок и позволяет определить, есть ли статистически значимая разница между двумя группами.
Еще одним распространенным критерием является непараметрический критерий Уилкоксона, который используется для сравнения двух зависимых выборок. Он анализирует разницу между парами наблюдений и позволяет выяснить, есть ли статистически значимая разница в двух группах.
Если требуется сравнить несколько групп между собой, то можно использовать критерий Краскелла-Уоллиса. Он расширяет критерий Манна-Уитни на случай более чем двух групп и позволяет проверить гипотезу о равенстве медиан сразу нескольких выборок.
В зависимости от постановки задачи и особенностей данных, может потребоваться выбор других критериев, таких как критерий Колмогорова-Смирнова, критерий Крускала-Уоллиса и др. Важно адекватно подобрать критерий, учитывая основные характеристики выборки и цель исследования.
| Критерий | Применение |
|---|---|
| Критерий Манна-Уитни | Сравнение двух независимых выборок |
| Критерий Уилкоксона | Сравнение двух зависимых выборок |
| Критерий Краскелла-Уоллиса | Сравнение более чем двух групп |
Таким образом, для выбора критерия при использовании непараметрических методов статистики необходимо анализировать характеристики данных и постановку задачи, а также учитывать особенности каждого конкретного критерия.
Статистические тесты для непараметрической статистики

Непараметрические методы статистики широко используются в случаях, когда данные не соответствуют предпосылкам параметрических моделей. Они позволяют анализировать и сравнивать данные без необходимости предполагать нормальное распределение или другие предпосылки.
Для проверки гипотез о распределении данных и сравнения нескольких групп непараметрические методы обеспечивают надежные результаты. В отличие от параметрических тестов, которые основаны на модели распределения данных, непараметрические статистические тесты предоставляют более гибкие возможности для анализа различных типов данных.
Одним из наиболее широко используемых непараметрических тестов является критерий Манна-Уитни. Он используется для сравнения двух независимых выборок и позволяет определить, есть ли статистически значимая разница между ними.
Другим часто применяемым непараметрическим тестом является критерий Уилкоксона для парных выборок. Он используется для сравнения двух связанных выборок, что позволяет определить, есть ли статистически значимая разница между двумя измерениями или условиями.
Также в непараметрической статистике используется критерий Фридмана для сравнения нескольких связанных выборок. Он может быть использован для определения различий в рангах несвязанных групп данных.
Для решения задачи общего сравнения нескольких независимых групп можно применить критерий Краскела-Уоллиса. Он позволяет определить, есть ли статистически значимые различия между группами.
Непараметрические тесты являются мощным инструментом для анализа данных, когда не выполняются предпосылки параметрических моделей. Они предоставляют возможность получить достоверные и надежные результаты, основанные на наблюдаемых данных.
| Тест | Описание |
|---|---|
| Критерий Манна-Уитни | Сравнение двух независимых выборок |
| Критерий Уилкоксона | Сравнение двух связанных выборок |
| Критерий Фридмана | Сравнение нескольких связанных выборок |
| Критерий Краскела-Уоллиса | Сравнение нескольких независимых групп |
Примеры применения непараметрических методов в исследованиях
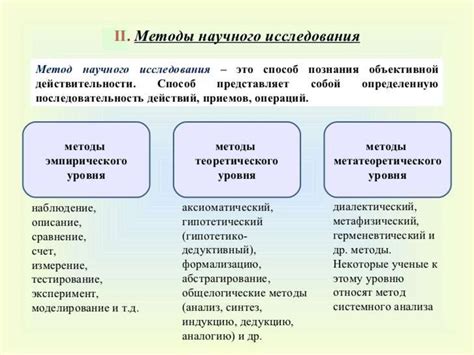
Непараметрические методы статистики находят широкое применение в различных исследованиях, где нет возможности предположить нормальное распределение данных или когда данные имеют нестандартную структуру. Вот несколько примеров применения непараметрических методов в исследованиях:
- Оценка медианы: непараметрические методы используются для оценки медианного значения, особенно в случаях, когда данные имеют тяжелые хвосты или наличие выбросов. Непараметрический критерий Манна-Уитни позволяет сравнить медианные значения для двух групп и определить, есть ли между ними статистически значимые различия.
- Сравнение распределений: если требуется сравнить два или более распределения, непараметрические тесты могут быть полезными. Ранговый или перестановочный тесты, такие как тест Манна-Уитни или Крускала-Уоллиса, позволяют сравнивать распределения без необходимости предполагать нормальность данных.
- Анализ связи без параметрических предположений: непараметрические методы могут использоваться для анализа связи между двумя переменными, когда нет возможности предположить линейную зависимость. Например, ранговый коэффициент корреляции Спирмена позволяет оценить связь между двумя переменными, измеренными в ранговой шкале.
- Выделение групп: кластерный анализ, основанный на непараметрических методах, позволяет выделить группы наблюдений на основе их сходства или различия. Непараметрические методы, такие как k-средних или метод ближайшего соседа, основаны на ранжировании данных и не требуют предположений о распределении или форме кластеров.
- Анализ выживаемости: непараметрические методы статистики также применяются в анализе выживаемости, когда исследуется время до наступления событий. Методы Каплана-Мейера и log-rank тест позволяют сравнивать группы наблюдений с учетом цензурированных данных и оценивать распределение выживаемости.



