Скобки являются важным инструментом в математике. Их использование позволяет установить порядок выполнения операций и правильно интерпретировать математические выражения. Однако, не всегда понятно, когда именно нужно ставить скобки, чтобы получить правильный результат.
Прежде всего, скобки используются для группировки операций. В математических выражениях, содержащих несколько операций, скобки позволяют определить приоритетное выполнение. Например, выражение (2 + 3) * 4 говорит нам о том, что сначала нужно сложить 2 и 3, а затем полученную сумму умножить на 4. Если бы скобки не были использованы, результат мог бы быть совсем другим.
Иногда, скобки используются для отделения частей выражения. Например, в выражении 2 * (3 + 4) скобки показывают, что сначала нужно выполнить операцию внутри скобок (сложить 3 и 4), а затем полученную сумму умножить на 2. Если бы скобки не были использованы, результат также мог бы быть иным.
Определенные правила существуют для определения порядка использования скобок в выражениях. Например, обычно скобки внутри выражений выполняются раньше. Однако, эти правила не всегда очевидны и приводят к разным интерпретациям выражений. Поэтому, важно понимать контекст и основные правила использования скобок, чтобы получить точный результат при решении математических задач.
Почему важно правильно ставить скобки в математике?

В математике, правильное использование скобок имеет центральное значение. Когда решается сложное математическое выражение, неправильная расстановка скобок может привести к неверному результату. Поэтому, чтобы получить правильный ответ, крайне важно знать, где и как ставить скобки.
Скобки используются для определения порядка выполнения математических операций в выражении. Важно помнить, что скобки определяют очередность операций и могут изменять результат вычислений. Например, выражение (2+3)×4 и 2+(3×4) имеют разные результаты из-за расстановки скобок.
Книга математических законов гласит: "Скобки всегда имеют приоритет над другими математическими операциями". Это означает, что все операции внутри скобок должны быть выполнены первыми, прежде чем продолжить вычисления. Если скобки расставлены неправильно, порядок операций может быть нарушен, что приведет к неверному ответу.
Правильно расставленные скобки также четко указывают, какие операции должны быть выполнены в первую очередь. Это помогает упростить сложные математические выражения и предотвратить ошибки в вычислениях.
Без правильной расстановки скобок может быть сложно сопоставить порядок выполнения операций. Это может создавать путаницу в вычислениях и затруднять понимание математических концепций.
Итак, правильное использование скобок в математике является фундаментальным навыком. Умение правильно ставить скобки позволит избежать ошибок в вычислениях и получить точный результат.
Когда скобки используются для приоритета операций

В математике скобки используются для установления приоритета операций. Они позволяют указать, какие операции нужно выполнить первыми.
Для примера, рассмотрим выражение:
2 + 3 * 4
Если бы скобок не было, то мы должны были бы сперва выполнить умножение, а затем сложение, получая в итоге 14.
Однако, если мы добавим скобки, выражение приобретет другой смысл:
(2 + 3) * 4
В этом случае мы должны выполнить сложение в скобках, получая 5, а затем умножить на 4, получая в итоге 20. Таким образом, порядок выполнения операций может быть изменен посредством скобок.
Правила приоритета операций
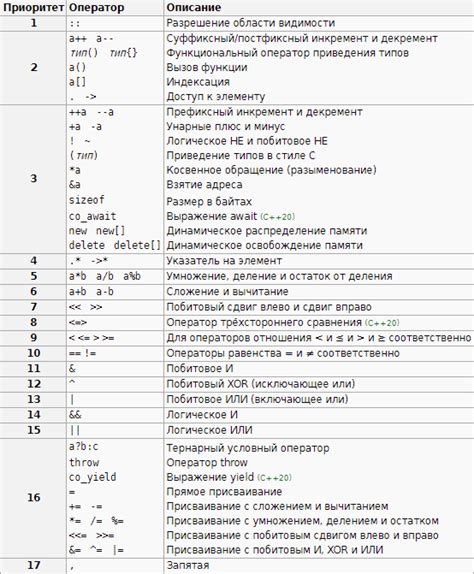
Математика строится на определенных правилах и порядке выполнения операций. Правила приоритета операций помогают определить, какие операции должны быть выполнены первыми при решении математического выражения или примера. Вот основные правила приоритета операций:
- Сначала выполняются операции в скобках.
- Затем выполняются операции с выражениями с высоким приоритетом: умножение и деление.
- После этого выполняются операции с выражениями с более низким приоритетом: сложение и вычитание.
- Если в выражении присутствуют операции с одинаковым приоритетом, то выполняются слева направо.
Например, если у нас есть пример 2 + 3 * 4, то сначала мы выполняем умножение, получаем 2 + 12, а затем сложение, в результате чего получаем 14. Если бы у нас были скобки, например (2 + 3) * 4, то мы бы сначала выполнели сложение в скобках, получили 5, а затем умножение, получили 20.
Выполняя операции в правильном порядке, мы получаем корректные результаты и избегаем путаницы. Знание правил приоритета операций очень важно при решении математических задач и примеров.
Когда скобки используются для уточнения выражений

В математике скобки ставятся для уточнения выражений и определения порядка операций. Они помогают указать, какие операции должны быть выполнены в первую очередь.
Скобки в выражениях могут быть круглыми (), квадратными [] или фигурными {}. В зависимости от их типа и расположения, математические выражения могут иметь различный смысл.
Круглые скобки () часто используются для группировки чисел или переменных, чтобы указать, что операции внутри скобок должны быть выполнены первыми. Например, выражение 2*(3+4) указывает, что сначала нужно выполнить операцию внутри скобок (3+4), а затем умножить результат на 2. В этом случае, результат будет равен 14.
Квадратные скобки [] могут использоваться для обозначения массивов в программировании. Они также могут использоваться в математических выражениях для обозначения промежутков или интервалов. Например, [1, 2, 3] обозначает массив с элементами 1, 2 и 3. А [0, 1] обозначает интервал от 0 до 1.
Фигурные скобки {} обычно используются для обозначения множества. Например, {1, 2, 3} обозначает множество с элементами 1, 2 и 3.
Использование скобок в математике позволяет уточнить выражения и избежать двусмысленности. Они являются важной частью математической нотации и часто используются при работе с выражениями и уравнениями.
Примеры уточнения выражений с помощью скобок

Скобки в математике используются для уточнения порядка выполнения операций или выделения частей выражения. Они помогают установить приоритетность операций и избежать различных неоднозначностей.
Ниже приведены некоторые примеры использования скобок:
- (3 + 4) * 2 - выражение в скобках будет вычислено первым, затем результат будет умножен на 2;
- 5 * (8 - 2) + 4 - сначала выражение в скобках будет вычислено, затем результат будет умножен на 5, после чего к нему будет прибавлено 4;
- 10 / (2 + 3) - сначала выражение в скобках будет вычислено, затем результат будет использован в делении на 10;
- (2 + 3) * (4 - 1) - оба выражения в скобках будут вычислены, затем их результаты будут перемножены.
Уточняйте выражения с помощью скобок, если требуется ясность и предотвращение ошибок при вычислениях. Знание правил приоритета операций и использование скобок помогут вам правильно интерпретировать и вычислить математические выражения.
Когда скобки используются для обозначения функций

В математических примерах скобки могут использоваться для указания аргументов внутри функции. Например, в функции f(x), скобки обозначают, что аргумент функции это x. При подстановке значения x в функцию, его необходимо заключить в скобки, чтобы показать, что это аргумент. Также скобки могут использоваться для группировки аргументов функций в сложных выражениях.
Скобки могут использоваться для обозначения различных типов функций, таких как:
1. Арифметические функции – такие функции, как сложение, вычитание, умножение и деление. Пример: f(x) = x + 1
2. Тригонометрические функции – функции, связанные с изучением треугольников и углов. Пример: sin(x), cos(x)
3. Логарифмические функции – функции, обратные экспоненциальным функциям. Пример: log(x)
4. Экспоненциальные функции – функции, в которых независимая переменная находится в показателе. Пример: f(x) = 2^(x)
5. Другие специальные функции, такие как квадратный корень, модуль числа и т.д.
Использование скобок для обозначения функций позволяет ясно и однозначно указать аргументы и значения функций. Это помогает упростить запись и решение математических задач.
Примеры использования скобок для обозначения функций

В математике скобки используются для обозначения функций и группировки операций. Они помогают четко определить порядок выполнения математических выражений и избежать неоднозначности. Вот несколько примеров использования скобок:
Пример 1:
Дано выражение: y = f(x)
Здесь скобки используются для обозначения функции f, которая принимает аргумент x. Скобки также могут использоваться для указания параметров функции.
Пример 2:
Дано выражение: y = (x + 2)(3x - 4)
Здесь скобки группируют операции сложения и вычитания. Сначала выполняется умножение внутри скобок, а затем остаток выражения. Без скобок порядок выполнения операций может быть неоднозначным.
Пример 3:
Дано выражение: y = x^2 + 2x + 1
Здесь скобки не используются, и результатом будет вычисление значений при помощи правил приоритета арифметических операций. Если нужно задать другой порядок выполнения операций, необходимо использовать скобки.
В общем, скобки играют важную роль в математике, позволяя ясно определить порядок операций и обозначить функции. Использование скобок в математических выражениях помогает избежать неоднозначности и получить правильные результаты.
Когда скобки используются для группировки элементов

В математике скобки используются для группировки элементов и определения порядка выполнения операций. Они помогают установить приоритеты и четко определить порядок операций в выражении.
Скобки могут использоваться для:
- Группировки операций: скобки используются для объединения элементов и определения порядка выполнения операций. Например, выражение (2 + 3) * 4 означает, что сначала выполняется операция внутри скобок, а затем результат умножается на 4.
- Указания аргументов: скобки используются для указания аргументов функций или операций. Например, функция с двумя аргументами может быть записана в виде f(x, y). Скобки позволяют явно указать значения аргументов и обозначить, какие операции должны быть выполнены.
- Определения множества: скобки могут быть использованы для определения множества элементов. Например, {1, 2, 3} обозначает множество из трех элементов.
Корректное использование скобок в математических выражениях позволяет установить ясные правила выполнения операций и предотвратить возникновение неоднозначностей.



