Квадратные уравнения – одна из основных тем в алгебре, которая является основой для изучения многих других математических дисциплин. В общем виде квадратное уравнение имеет вид ax^2 + bx + c = 0, где a, b и c – коэффициенты, причем a не может быть равным нулю. Однако в некоторых случаях дискриминант этого уравнения может оказаться равным нулю. Рассмотрим несколько примеров таких уравнений.
Примером квадратного уравнения с нулевым дискриминантом может быть уравнение x^2 - 4x + 4 = 0. Здесь a = 1, b = -4, c = 4. Дискриминант уравнения равен b^2 - 4ac = (-4)^2 - 4*1*4 = 0, что подтверждает нулевое значение. Решение данного уравнения сводится к нахождению корня уравнения x = -b/2a. В данном случае, x = 4/2*1 = 2.
Еще одним примером квадратного уравнения с нулевым дискриминантом может быть уравнение 3x^2 - 6x + 3 = 0. Тут a = 3, b = -6, c = 3. Дискриминант уравнения равен (-6)^2 - 4*3*3 = 0, что также дает нам нулевое значение. Решением этого уравнения, аналогично предыдущему, является x = -b/2a. Следовательно, x = 6/2*3 = 1.
Уравнение с нулевым дискриминантом: определение
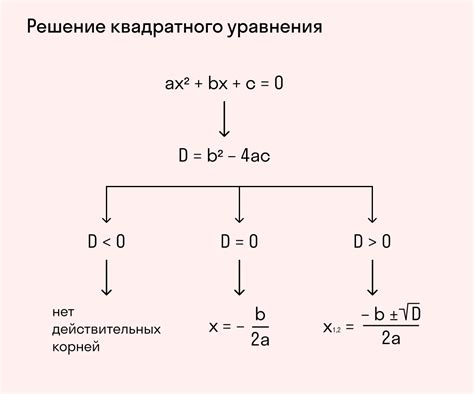
Дискриминант квадратного уравнения вычисляется по формуле:
Д = b² - 4ac
Если дискриминант равен нулю, то это означает, что у уравнения есть только один действительный корень. В этом случае график квадратного уравнения будет касаться оси абсцисс в точке этого корня.
Интересно, что уравнение с нулевым дискриминантом можно записать в виде (x - p)² = 0, где p - значение корня. Такое уравнение называется уравнением с двойным корнем.
Примеры квадратных уравнений с нулевым дискриминантом:
- x² - 2x + 1 = 0
- 4x² - 12x + 9 = 0
- 9x² + 12x + 4 = 0
Пример 1: один корень уравнения
Уравнение: x2 - 4x + 4 = 0
Для вычисления корня данного уравнения можно воспользоваться формулой: x = -b / (2a), где a и b - коэффициенты при x2 и x соответственно.
В данном уравнении a = 1 и b = -4. Подставим значения в формулу и найдем значение корня:
x = -(-4) / (2 * 1) = 4 / 2 = 2
Таким образом, уравнение x2 - 4x + 4 = 0 имеет один корень x = 2.
Пример 2: комплексные корни уравнения
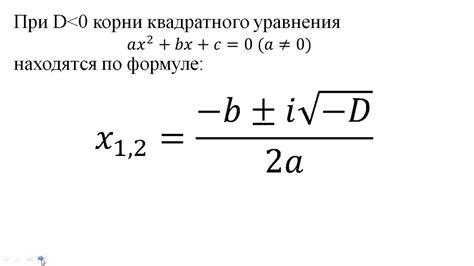
Рассмотрим, например, уравнение x2 + 4 = 0. В этом уравнении коэффициент при x равен 1, коэффициент при x2 равен 0, а свободный член равен 4.
Дискриминант уравнения можно вычислить по формуле: Д = b2 - 4ac. Подставив значения коэффициентов уравнения, получим: Д = 02 - 4 * 1 * 4 = -16.
В данном случае, дискриминант отрицательный, что означает, что уравнение имеет два комплексных корня. Обозначим их как x1 и x2.
Комплексные корни уравнения могут быть представлены в виде: x1, x2 = -b ± √(D) / 2a. Подставляя значения коэффициентов и дискриминанта, получим: x1, x2 = -0 ± √(-16) / 2 * 1.
Извлекая корень из отрицательного числа, получим x1, x2 = 0 ± 4i / 2, где i - это мнимая единица, такая, что i2 = -1.
Таким образом, корни уравнения x2 + 4 = 0 будут представлены как x1 = 2i и x2 = -2i.
Пример 3: бесконечно много корней уравнения

Рассмотрим квадратное уравнение:
x2 - 6x + 9 = 0
Вычисляя дискриминант по формуле, получим:
D = b2 - 4ac = (-6)2 - 4(1)(9) = 0
Таким образом, дискриминант равен нулю.
Подставляя значения в уравнение, получаем:
x2 - 6x + 9 = 0
Выражение в левой части уравнения можно преобразовать следующим образом:
x2 - 6x + 9 = (x - 3)2 = 0
Из этого преобразования следует, что квадратный корень из обеих частей уравнения будет равен:
x - 3 = 0
x = 3
Таким образом, уравнение имеет бесконечно много корней, так как любое значение x, равное 3, является корнем уравнения.
Пример 4: нулевой коэффициент при x в квадрате

Решим данное уравнение. Поскольку коэффициент при x^2 равен нулю, получаем уравнение 5x - 6 = 0. Здесь коэффициент при x равен 5, а свободный член равен -6.
Для решения данного линейного уравнения нам необходимо выразить x. Перенесем -6 в правую часть уравнения: 5x = 6. Затем разделим обе части уравнения на 5: x = 6/5.
Таким образом, корень данного квадратного уравнения с нулевым дискриминантом равен x = 6/5.
Пример 5: квадратное уравнение в форме с предварительным приведением

Представим, что у нас есть квадратное уравнение следующего вида:
3x2 - 6x + 3 = 0
Прежде чем решить это уравнение, приведем его к удобной форме. Мы видим, что все коэффициенты делятся на 3. Таким образом, мы можем разделить все уравнение на 3:
x2 - 2x + 1 = 0
Теперь, когда у нас есть уравнение в удобной форме, мы можем продолжить с его решением. Раскроем скобки:
| x2 | - 2x | + 1 |
|---|---|---|
| x | - 1 | |
| x | - 1 | |
| - 1 |
Теперь, чтобы решить уравнение, мы получаем:
(x - 1)(x - 1) = 0
Чтобы получить два корня, уравнение равно 0, когда каждый из множителей равен 0:
x - 1 = 0
Или
x - 1 = 0
Таким образом, у нас есть два корня:
x = 1
Уравнение имеет два равных корня, так как дискриминант равен нулю.
Пример 6: использование формулы для корней

Если у квадратного уравнения с нулевым дискриминантом коэффициент a не равен нулю, корни можно найти с помощью формулы:
x = -b / 2a
Давайте рассмотрим пример:
Уравнение: x^2 - 6x + 9 = 0
Коэффициенты: a = 1, b = -6, c = 9
Подставляем значения в формулу и находим корни:
x = (-(-6)) / (2 * 1) = 6 / 2 = 3
Ответ: уравнение имеет один корень x = 3.



