Проценты с непрерывным наращиванием или дисконтированием – это одна из основных концепций финансовой математики, которая находит широкое применение в различных сферах, от финансовой аналитики и инвестиционного планирования до банковского дела и актуарных расчетов. Этот метод представляет собой способ измерения изменения стоимости денег во времени.
Основной принцип процентов с непрерывным наращиванием лежит в основе формулы непрерывного наращивания или дисконтирования процентной ставки. При этом, процентная ставка представляет собой денежную компенсацию за использование капитала или за отказ от него. В свою очередь, эта компенсация представлена двумя основными составляющими: процентной ставкой и временем.
Основная формула процентов с непрерывным наращиванием или дисконтированием выглядит следующим образом: FV = PV * e^(r * t), где FV – будущая стоимость, PV – настоящая стоимость, r – процентная ставка, t – время.
Одним из наиболее интересных применений процентов с непрерывным наращиванием является финансовая аналитика, которая позволяет оценить доходность и рентабельность инвестиций в долгосрочной и краткосрочной перспективе. Кроме того, этот метод находит применение и в банковском деле, где используется для расчета доходности по депозитам и кредитам, а также для анализа рисков и определения стоимости капитала.
Основные принципы и формулы непрерывного наращивания или дисконтирования процентов

Проценты с непрерывным наращиванием или дисконтированием представляют собой особый вид расчетов процентных ставок, где проценты начисляются или учитываются непрерывно в течение определенного периода времени.
Одной из основных формул для расчета непрерывного наращивания или дисконтирования процентов является формула непрерывного процента:
Непрерывный процент: | A = P * ert |
Где:
- A - конечная сумма или будущая стоимость инвестиции;
- P - начальная сумма или текущая стоимость инвестиции;
- e - основа натурального логарифма, приближенно равная 2,71828;
- r - процентная ставка;
- t - период времени, выраженный в годах.
Также существует формула для расчета дисконтирования процентов:
Обратный процент: | P = A * e-rt |
Где значения переменных обозначены так же, как и в формуле непрерывного процента.
Принципы непрерывного наращивания или дисконтирования процентов универсальны и могут применяться в различных сферах, включая финансы, экономику и математику. Эти формулы позволяют точно рассчитать будущую стоимость инвестиции или ее текущую стоимость на основе заданной процентной ставки и временного периода.
Проценты и их значение в экономике

В экономике проценты играют ключевую роль во многих аспектах. Например, они определяют ставки по кредитам и займам, влияют на инвестиционные решения предприятий, а также влияют на эффективность денежно-кредитной политики государства.
Проценты могут варьироваться в зависимости от условий рынка, инфляции, политики Центрального банка и других факторов. Их изменение может оказывать существенное воздействие на экономическую активность и инфляцию.
Чтобы эффективно управлять финансами и понимать связь между временем и деньгами, необходимо разбираться в принципах работы процентов и их формулах. Например, формула наращенного процента позволяет рассчитать будущую стоимость вклада или долга с учетом процентной ставки и времени.
Также стоит упомянуть о дисконтировании процентов, которое является обратным процессом наращивания процентов. Дисконтирование используется, чтобы определить приведенную стоимость будущих денежных потоков или оценить стоимость активов.
Итак, проценты – это неотъемлемая часть экономической системы, которая оказывает влияние на различные финансовые решения и позволяет оценить стоимость времени и денег.
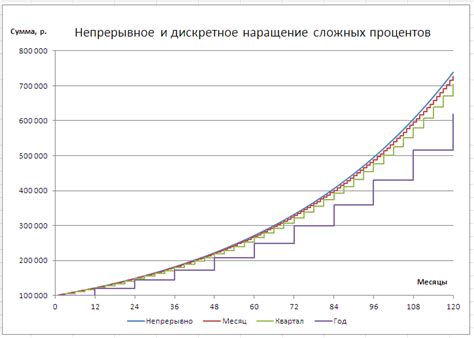
Непрерывное наращивание процентов: основное понятие и примеры
Формула для расчета будущей стоимости на основе непрерывного наращивания процентов выглядит следующим образом:
- P = P0 * er*t
где:
- P - будущая стоимость
- P0 - текущая стоимость или начальная сумма
- e - основание натурального логарифма (приблизительно равно 2,718281828)
- r - процентная ставка
- t - период времени
Пример использования формулы:
Предположим, что у вас есть сумма в размере 1000 долларов и вы хотите рассчитать ее будущую стоимость через 5 лет по процентной ставке 5%.
Используя формулу, мы можем рассчитать будущую стоимость:
- P = 1000 * e0.05*5 ≈ 1284.03
Таким образом, через 5 лет ваша сумма в размере 1000 долларов вырастет до примерно 1284.03 долларов при данной процентной ставке.
Непрерывное наращивание процентов является важным инструментом для финансовых расчетов и позволяет предсказывать будущую стоимость денежных сумм на основе процентной ставки и периода времени. Этот метод позволяет лучше понять и анализировать финансовые вопросы и принимать обоснованные решения в области инвестиций и кредитования.
Формула для расчета суммы с учетом непрерывного наращивания процентов

S = P * e^(rt)
где:
- S – итоговая сумма, которую мы получим в результате наращивания процентов;
- P – изначальная сумма или начальный капитал;
- e – основание натурального логарифма, приближенное значение которого равно около 2,71828;
- r – процентная ставка, выраженная в виде десятичной дроби;
- t – время или период в годах.
Применение данной формулы позволяет рассчитать итоговую сумму, которую мы получим после определенного времени с использованием непрерывного наращивания процентов. При этом, формула учитывает такие параметры, как начальный капитал, процентная ставка и время.
Непрерывное наращивание процентов является более точным методом расчета, чем дискретное наращивание, так как проценты начисляются непрерывно и позволяют получить более точные результаты.
Дисконтирование процентов: принципы и области применения

Дисконтирование процентов находит широкое применение в различных областях, включая финансовую математику, экономику, инвестиции и управление финансами. Оно позволяет оценить стоимость будущих денежных потоков и принять правильные финансовые решения.
Одним из основных инструментов дисконтирования процентов является дисконтирование денежных потоков. Этот метод позволяет определить стоимость будущих денежных потоков путем приведения их к настоящей стоимости с учетом процентной ставки.
Дисконтирование процентов также используется при оценке инвестиционных проектов. Оно позволяет определить, какая часть денежных поступлений от проекта должна быть получена в настоящее время, чтобы он был финансово выгодным. Таким образом, дисконтирование процентов помогает принимать решения о выборе наиболее выгодных проектов и оптимальном использовании ресурсов.
Другой областью применения дисконтирования процентов является определение стоимости активов и обязательств компании. Дисконтирование процентов позволяет оценить текущую стоимость будущих платежей или поступлений по активам или обязательствам, учитывая их сроки и процентные ставки. Эта информация помогает компаниям принимать финансовые решения и планировать свою деятельность.
Таким образом, дисконтирование процентов является важным инструментом финансового анализа и принятия решений. Понимание его принципов и областей применения позволяет эффективно управлять финансовыми ресурсами и принимать обоснованные финансовые решения.
Формула для расчета дисконтированной суммы с учетом процентов

Для расчета дисконтированной суммы с учетом процентов необходимо использовать формулу:
V = C / (1 + r)^t
где:
V - дисконтированная сумма,
C - начальная сумма (или будущая сумма, в зависимости от задачи),
r - процентная ставка помесячно (годовая ставка делится на 12),
t - количество периодов.
Эта формула позволяет учесть процентные начисления или дисконтирование в течение нескольких периодов.
Например, предположим, у нас есть начальная сумма в размере 10000 рублей, которую мы хотим дисконтировать на протяжении 5 лет по ставке 6% в год. Дисконтированная сумма будет равняться:
V = 10000 / (1 + 0.06/12)^(5*12) = 7472.24 рублей
Таким образом, дисконтированная сумма составляет 7472.24 рублей.
Эта формула позволяет сделать расчеты более точными, учитывая изменение ставки процента и периодов.



