Ортогональные векторы - это важное понятие в линейной алгебре, которое находит применение во многих областях науки и техники. Ортогональные векторы означают, что они перпендикулярны друг другу, и у них нулевое скалярное произведение.
Проверка ортогональности двух векторов может быть выполнена несколькими методами. Один из таких методов - вычисление скалярного произведения векторов и проверка его равенства нулю. Если скалярное произведение равно нулю, то векторы ортогональны. Этот метод является наиболее простым и прямолинейным, хотя его применимость ограничена одномерным пространством.
Другой метод проверки ортогональности векторов - использование геометрических свойств. Например, если два вектора имеют перекрестное направление, то они точно являются ортогональными. Кроме того, можно использовать свойства ортогональности для проверки ортогональности векторов в трехмерном пространстве.
В данной статье мы рассмотрим различные методы проверки ортогональности двух векторов и их применение в практических задачах. Мы также приведем примеры и наглядные иллюстрации для лучшего понимания этой важной математической концепции.
Определение ортогональности векторов

Ортогональность двух векторов в геометрии означает, что они перпендикулярны друг другу, то есть образуют прямой угол между собой. Для проверки ортогональности векторов необходимо использовать определенные методы.
Первый метод основан на определении векторного произведения двух векторов. Если векторное произведение равно нулевому вектору, то векторы ортогональны. Формула для нахождения векторного произведения векторов a и b выглядит следующим образом:
a × b = |a| |b| sin(θ) n
где |a| и |b| - длины векторов a и b, θ - угол между векторами, n - единичный вектор, перпендикулярный плоскости, в которой лежат a и b.
Второй метод основан на вычислении скалярного произведения векторов. Если скалярное произведение равно нулю, то векторы ортогональны. Формула для скалярного произведения векторов a и b выглядит следующим образом:
a · b = |a| |b| cos(θ)
где |a| и |b| - длины векторов a и b, θ - угол между векторами.
Проверка ортогональности векторов может быть полезна во многих областях, таких как геометрия, физика, компьютерная графика и многие другие.
Понятие ортогональности

Чтобы проверить ортогональность двух векторов, используется так называемое "правило скалярного произведения". Скалярное произведение двух векторов определяется как сумма произведений их соответствующих координат.
Если скалярное произведение равно нулю, то векторы ортогональны. То есть, если векторы A и B заданы как A = (a1, a2, a3) и B = (b1, b2, b3), то скалярное произведение можно записать так:
A · B = a1 * b1 + a2 * b2 + a3 * b3
Если скалярное произведение равно 0:
A · B = 0
то это означает, что векторы A и B ортогональны.
Ортогональность векторов широко применяется в математике, физике, графике и других областях, где важно определить взаимное положение объектов в пространстве. Например, при построении трехмерной модели или определении направлений движения.
Свойства ортогональных векторов
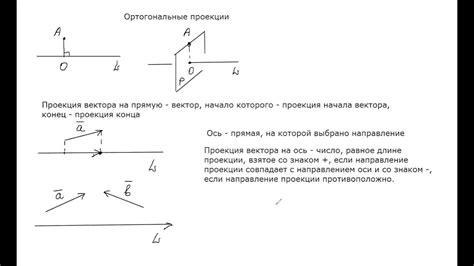
1. Ортогональные векторы перпендикулярны друг другу.
Если два вектора ортогональны, то они образуют прямой угол, то есть угол между ними равен 90 градусам. Это означает, что линии, построенные по этим векторам, пересекаются под прямым углом.
2. Скалярное произведение ортогональных векторов равно 0.
Если векторы a и b ортогональны, то их скалярное произведение равно нулю. Скалярное произведение определяется как произведение длин векторов и косинуса угла между ними. Поскольку угол между ортогональными векторами равен 90 градусам, косинус этого угла равен 0, и произведение длин векторов на 0 дает 0.
3. Ортогональные векторы независимы.
Ортогональные векторы являются линейно независимыми, то есть ни один из них не может быть выражен через другие с помощью линейной комбинации. Для двухмерного пространства это означает, что они не лежат на одной прямой. В трехмерном пространстве ортогональность означает, что векторы не лежат на одной плоскости.
4. Ортогональные векторы образуют базис векторного пространства.
Множество ортогональных векторов, имеющих ненулевую длину, образует базис векторного пространства. Это означает, что каждый вектор в этом пространстве может быть представлен как линейная комбинация этих ортогональных векторов.
5. Ортогональные векторы используются в различных областях математики и физики.
Ортогональность векторов играет важную роль во многих областях науки, включая геометрию, физику, инженерию и компьютерную графику. Она используется в задачах нахождения координат, решения систем линейных уравнений, описания движения и взаимодействия объектов и многих других.
Методы проверки ортогональности
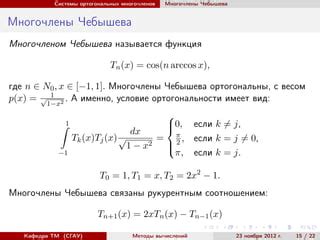
Метод векторного произведения
Один из самых распространенных методов проверки ортогональности - это использование векторного произведения. Если два вектора A и B ортогональны, то их векторное произведение (A × B) будет равно нулевому вектору (0, 0, 0). Таким образом, для проверки ортогональности можно вычислить векторное произведение данных векторов и проверить, равен ли результат нулевому вектору.
Метод скалярного произведения
Другой метод проверки ортогональности - использование скалярного произведения. Если два вектора A и B ортогональны, то их скалярное произведение (A • B) будет равно нулю. При проверке ортогональности можно вычислить скалярное произведение данных векторов и проверить, равно ли оно нулю.
Метод угла между векторами
Третий метод проверки ортогональности - это использование угла между векторами. Если два вектора A и B являются ортогональными, то угол между ними будет равен 90 градусам или π/2 радиан. Для проверки ортогональности можно вычислить угол между данными векторами и проверить, равен ли он 90 градусам или π/2 радиан.
Указанные методы позволяют проверить ортогональность двух векторов и являются базовыми инструментами в линейной алгебре. При работе с векторами важно учитывать их размерность и правильно применять соответствующий метод проверки ортогональности.
Геометрический метод
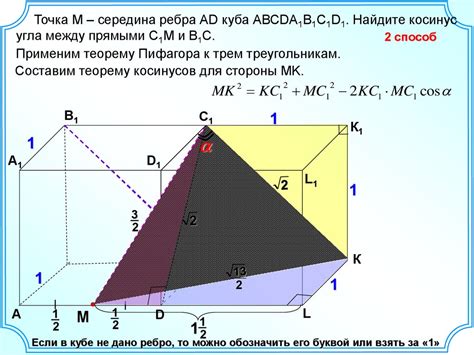
Геометрический метод проверки ортогональности двух векторов основан на геометрической интерпретации понятия "ортогональность". Два вектора считаются ортогональными, если они перпендикулярны друг другу.
Чтобы проверить ортогональность двух векторов с помощью геометрического метода, можно построить эти векторы на координатной плоскости и проверить перпендикулярность с помощью углового косинуса.
Допустим, у нас есть два вектора A и B. Чтобы проверить их ортогональность, мы можем найти их скалярное произведение. Если скалярное произведение равно нулю, то векторы ортогональны. Иначе, если скалярное произведение не равно нулю, то векторы не ортогональны.
Если скалярное произведение двух векторов равно нулю, это означает, что угол между ними равен 90 градусов, то есть они перпендикулярны друг другу.
Например, пусть у нас есть два вектора A(2, 4) и B(4, -2). Мы можем найти их скалярное произведение путем перемножения соответствующих координат и сложения результатов: A•B = (2 * 4) + (4 * -2) = 8 - 8 = 0. Так как результат скалярного произведения равен нулю, мы можем заключить, что векторы A и B ортогональны.



