Прямоугольник – это одна из основных фигур в геометрии, в которой все углы равны по 90 градусов, что делает его идеальной формой для множества приложений и задач. Прямоугольник можно описать как четырехугольник с противоположными сторонами, которые параллельны и имеют одинаковую длину. Все его стороны также перпендикулярны друг к другу.
Главное свойство прямоугольника – равенство всех углов, которые являются прямыми. Это дает нам возможность вывести множество теорем и формул, которые помогут нам решать задачи с прямоугольниками. Например, мы можем использовать теорему Пифагора для нахождения длины диагонали прямоугольника, если известны длины его сторон.
Прямоугольники широко применяются в архитектуре, строительстве, геометрии и других областях. Они служат основой для создания практически любого здания или конструкции. Например, большинство домов и зданий имеют прямоугольную форму своих стен и крыши. Также, прямоугольники используются в компьютерной графике для создания и отображения объектов различных форм и размеров.
Определение прямоугольника

Прямоугольник можно задать по длинам его сторон. Если a - длина одной стороны, а b - длина другой стороны, то его площадь S равна произведению длин сторон: S = a * b. Периметр прямоугольника P вычисляется по формуле P = 2 * (a + b).
Прямоугольники используются в различных областях, таких как архитектура, строительство, дизайн, геометрия и многие другие. Они широко применяются при решении задач, связанных с вычислением площади, периметра, объема, а также при создании диаграмм и графиков.
Примеры прямоугольников включают окна, двери, тетради, столы и многие другие предметы. Также в геометрии существуют специальные типы прямоугольников, такие как квадрат (прямоугольник со сторонами, равными друг другу), и прямоугольник со всеми сторонами разной длины.
Свойства прямоугольника
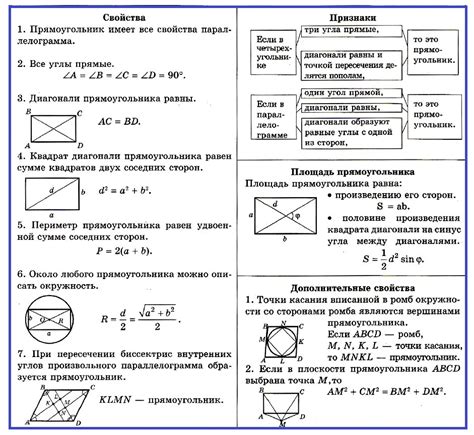
- Противоположные стороны прямоугольника равны по длине и параллельны друг другу.
- Диагонали прямоугольника равны по длине и делят его на два равносильных треугольника.
- Периметр прямоугольника равен сумме всех его сторон.
- Площадь прямоугольника равна произведению длины его сторон.
- Для прямоугольника существует формула Пифагора, которая связывает длины его сторон: a^2 + b^2 = c^2, где a и b - стороны прямоугольника, а c - его диагональ.
Прямоугольники встречаются в различных областях жизни и науки, их свойства широко применяются в геометрии, строительстве, физике, компьютерной графике и многих других областях.
Примеры прямоугольников в геометрии
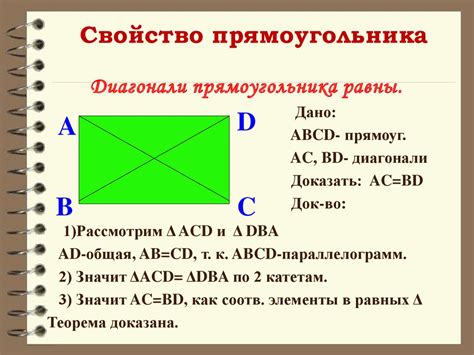
Прямоугольник ABCD:
В данном примере прямоугольник ABCD имеет стороны AB и BC, параллельные сторонам CD и AD соответственно. Углы A, B, C и D равны по 90 градусов, что делает этот четырёхугольник прямоугольным.
Прямоугольник PQRS:
Прямоугольник PQRS также соответствует определению прямоугольника. В этом примере стороны PQ и RS параллельны сторонам QR и PS, а углы P, Q, R и S равны 90 градусам.
Прямоугольник XYZW:
Этот прямоугольник имеет противоположные стороны XY и WZ, а также стороны XZ и YW, которые параллельны друг другу. Углы X, Y, Z и W равны 90 градусам, что делает данный четырёхугольник прямоугольным.
Прямоугольники широко используются в геометрии и имеют множество применений в различных областях, включая строительство, дизайн и научные исследования.
Геометрическое представление прямоугольника
Геометрическое представление прямоугольника можно визуализировать с помощью следующих свойств:
- Четыре угла прямые. Каждый угол равен 90 градусов, что делает прямоугольник прямоугольным.
- Противоположные стороны параллельны. Это означает, что две горизонтальные и две вертикальные стороны прямоугольника расположены параллельно друг другу.
- Противоположные стороны равны. Это свойство означает, что две противоположные горизонтальные стороны прямоугольника равны по длине, а также две противоположные вертикальные стороны равны по длине.
- Длина стороны прямоугольника может быть больше или меньше ширины, но углы остаются прямыми и все стороны остаются параллельными.
Примеры геометрических представлений прямоугольника включают дверные и оконные проемы, столы, рамы для фотографий и многие другие предметы, имеющие прямоугольную форму.



