Параллелограмм - это особый вид четырехугольника, у которого противоположные стороны параллельны и равны. Одним из основных свойств параллелограмма является равенство противоположных углов. Это значит, что две противоположные вершины параллелограмма соединены одной диагональю, и углы, образованные этой диагональю с противоположными сторонами, равны между собой.
Доказательство равенства противоположных углов в параллелограмме основывается на свойствах параллельных прямых и сходстве треугольников. Для доказательства проводится дополнительная прямая, соединяющая противоположные вершины параллелограмма. Получившийся треугольник разбивается на два других треугольника, которые считаются сходными по двум сторонам и углу между ними. Из сходства треугольников следует, что углы, образованные дополнительной прямой с противоположными сторонами параллелограмма, равны между собой.
Равенство противоположных углов в параллелограмме является важным свойством и используется при решении различных геометрических задач. Оно позволяет находить значения углов, зная только один из них, а также применять его для доказательства других свойств параллелограмма. Поэтому понимание этого свойства является необходимым при изучении геометрии и ее применении в практических задачах.
Свойство параллелограмма
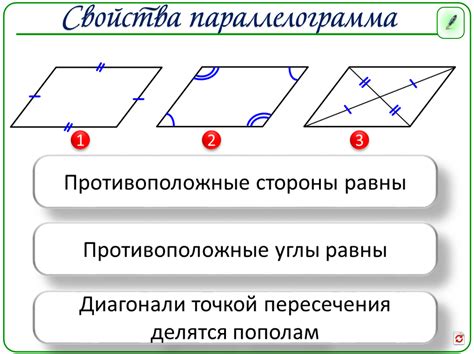
Свойство равенства противоположных углов в параллелограмме гласит: "Углы, расположенные у основания параллелограмма и прилегающие к одной из его сторон, равны между собой". Иными словами, углы, лежащие на одной основании параллелограмма и примыкающие к параллельным сторонам, равны.
Это свойство можно объяснить с помощью параллельных прямых. Пусть AB и CD - параллельные стороны параллелограмма, AD и BC - его основания. Также пусть E и F - точки пересечения диагоналей AC и BD с сторонами AB и CD соответственно. Тогда углы AED и BFC, лежащие на основаниях AD и BC, равны, так как они являются вертикальными углами.
| Углы параллелограмма | Описание |
|---|---|
| Противоположные углы | Углы, расположенные у противоположных сторон параллелограмма, равны. |
| Смежные углы | Углы, лежащие на одной стороне параллелограмма и имеющие общую вершину, дополняют друг друга до 180 градусов. |
| Углы на одной базе | Углы, лежащие на одной основе параллелограмма и прилегающие к параллельным сторонам, равны. |
Свойство равенства противоположных углов в параллелограмме является одним из основных и помогает в решении задач на нахождение углов этой фигуры. Оно позволяет упростить задачу, делая ее более прозрачной и понятной.
Геометрическое определение

Прямоугольник является одним из видов параллелограммов, поэтому этот закон верен и для прямоугольников. Прямоугольник имеет четыре прямых угла, и все они равны друг другу.
Для параллелограмма доказательство этого закона основывается на свойствах параллельных линий и соотношениях угловых величин.
Чтобы визуализировать, пусть у нас есть параллелограмм ABCD. Пусть угол DAB обозначен как α, а угол ABC обозначен как β. Тогда мы можем заявить, что угол BCD также равен α, а угол CDA равен β.
- Угол ABC и угол BCD являются вертикальными углами, а значит, они равны между собой.
- Угол DAB и угол CDA являются вертикальными углами, а значит, они равны между собой.
- Угол DAB и угол ABC являются соответственными углами, поскольку они находятся на параллельных линиях AB и CD и пересекаются с третьей линией AD.
- Угол CDA и угол BCD являются соответственными углами, поскольку они находятся на параллельных линиях AD и BC и пересекаются с третьей линией CD.
Таким образом, из этих свойств между углами параллелограмма можно заключить, что оба противоположных угла параллелограмма равны.
Связь с другими свойствами
Свойство равенства противоположных углов в параллелограмме тесно связано с другими свойствами этой фигуры. Рассмотрим такие связи:
| Свойство | Описание |
|---|---|
| Равенство диагоналей | В параллелограмме диагонали равны между собой и делятся пополам. |
| Равенство противоположных сторон | Параллелограмм имеет противоположные стороны, которые равны между собой. |
| Соотношение сторон и углов | В параллелограмме соседние углы смежных сторон дополняют друг друга до 180 градусов, а соответствующие углы равны. |
Эти свойства легко доказываются с использованием определений и свойств параллелограмма. Так, если противоположные углы равны, то параллелограмм может быть также доказан симметричными свойствами его сторон, диагоналей и углов.
Понимание связи между этими свойствами позволяет более полно изучить и использовать параллелограммы в разных математических задачах и конструкциях.
Доказательство равенства
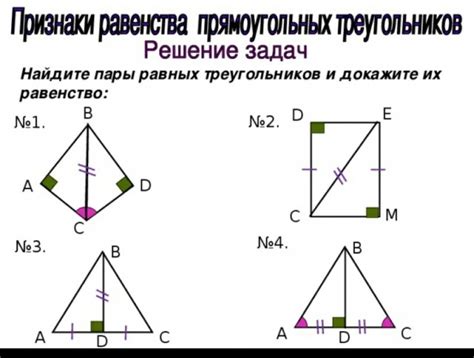
Равенство противоположных углов в параллелограмме может быть доказано с помощью нескольких фактов и теорем, связанных с параллельными прямыми и углами.
Для начала, вспомним основные свойства параллелограмма:
- Противоположные стороны параллельны и равны.
- Противоположные углы параллельны и равны.
- Сумма углов в параллелограмме равна 360 градусов.
Из этих свойств следует, что противоположные углы в параллелограмме должны быть равны.
Пусть у нас есть параллелограмм ABCD. Рассмотрим две стороны этого параллелограмма - сторону AB и сторону CD. По свойству 1 параллелограмма, эти стороны параллельны.
Мы знаем, что угол BCA и угол ADC являются противоположными углами в параллелограмме ABCD. Согласно свойству 2 параллелограмма, эти углы должны быть равны.
Аналогично, угол CDA и угол CAB являются противоположными углами параллелограмма ABCD и, следовательно, они также равны.
Таким образом, мы доказали, что противоположные углы в параллелограмме ABСD равны друг другу.
Данное доказательство позволяет нам утверждать, что равенство противоположенных углов в параллелограмме является одним из основных свойств данной фигуры.
Примеры решения задач

В данном разделе представлены примеры решения задач, связанных с равенством противоположных углов в параллелограмме. Рассмотрим несколько задач.
- Задача 1. Дан параллелограмм ABCD, в котором угол B равен 60 градусов. Найдите меру угла D.
- Задача 2. В параллелограмме ABCD угол D равен 120 градусов. Найдите меру угла C.
- Задача 3. В параллелограмме ABCD углы A и B равны. Найдите меру каждого из этих углов.
Решение: так как углы AB и CD являются противоположными, то они равны между собой. Известно, что угол B равен 60 градусов. Так как сумма углов треугольника равна 180 градусам, то угол BAD равен (180 - 60) / 2 = 60 градусов. Таким образом, мера угла D равна 60 градусов.
Решение: так как углы AD и BC являются противоположными, то они равны между собой. Известно, что угол D равен 120 градусов. Так как сумма углов треугольника равна 180 градусам, то угол BAC равен (180 - 120) / 2 = 30 градусов. Таким образом, мера угла C равна 30 градусов.
Решение: так как углы AD и BC являются противоположными, то они равны между собой. Из условия исходит, что углы A и B равны. Обозначим их меру через x. Так как сумма углов треугольника равна 180 градусам, то имеем уравнение: 2x = 180, откуда x = 90 градусов. Таким образом, мера каждого из углов A и B равна 90 градусов.
Таким образом, решение задач, связанных с равенством противоположных углов в параллелограмме, требует применения знания о сумме углов треугольника и свойствах параллелограмма.
Резюме

Равенство противоположных углов в параллелограмме можно объяснить с помощью двух треугольников. Если мы проведем диагональ в параллелограмме, то он разделит фигуру на два треугольника. Так как противоположные стороны параллелограмма равны, то треугольники, образованные диагональю и этими сторонами, будут равнобедренными. А в равнобедренном треугольнике углы при основании равны. Таким образом, углы, образованные диагональю и соответствующими сторонами параллелограмма, будут равны между собой.
Равенство противоположных углов в параллелограмме является важным свойством, которое позволяет проводить различные геометрические доказательства и вычисления. Оно используется в математике и строительстве, а также может быть полезным при решении различных задач и заданий.
Противоположные углы в параллелограмме:
|




