Дробь - это одна из важнейших математических концепций, которая позволяет осуществлять деление чисел. Как правило, числитель и знаменатель в дроби представляют собой ненулевые числа. Однако, возникает вопрос: существует ли дробь с числителем, равным нулю?
Ответ на этот вопрос прост и однозначен: да, дробь с числителем равным нулю существует. Такая дробь называется нулевой или нулевым делителем. Она обозначается как 0/х, где х - произвольное ненулевое число.
Что такое дробь в математике?

В дроби числитель и знаменатель могут быть представлены целыми числами или десятичными дробями. Например, дробь 3/4 означает, что мы рассматриваем три части целого, которое разделено на четыре равные части.
Дроби могут быть положительными или отрицательными, в зависимости от знака числителя и знаменателя. Например, дробь -2/5 означает, что мы рассматриваем две отрицательные части целого, которое разделено на пять равных частей.
Дроби могут быть использованы для представления различных математических концепций, таких как частота, вероятность, проценты и доли. Они также используются для выполнения различных операций, таких как сложение, вычитание, умножение и деление.
Разбираем понятие дроби

В дроби нет ограничений на значения числителя и знаменателя, они могут быть любыми целыми или дробными числами. Числом над знаком дроби может быть любое число, а числом под знаком дроби - любое ненулевое число.
Дроби можно классифицировать на натуральные, целые, рациональные, иррациональные и действительные. Натуральные дроби имеют единичную целую часть, целые дроби представляют собой числа с нулевой дробной частью, рациональные дроби могут быть записаны в виде обыкновенной или десятичной дроби, иррациональные дроби имеют бесконечное число десятичных знаков, а действительные дроби включают в себя как рациональные, так и иррациональные числа.
Дробь с числителем, равным нулю, называется нулевой дробью. В математике ее записывают как 0/знаменатель. Такая дробь существует и равна нулю, так как ноль разделенный на любое ненулевое число всегда будет равен нулю.
Важно отметить, что деление на ноль, то есть дробь с нулевым знаменателем, невозможно в математике, так как не имеет смысла. В этом случае мы говорим об "неопределенной дроби" или "делении на ноль", и она не имеет значений или свойств.
Какие свойства имеет дробь?

Свойства дроби:
1. Числитель и знаменатель. Каждая дробь состоит из числителя и знаменателя. Числитель показывает, сколько частей имеется, а знаменатель указывает на количество частей, на которые число делится.
2. Знак. Дробь может быть положительной или отрицательной. Знак дроби определяется знаком числителя. Если числитель положительный, то вся дробь положительная. Если числитель отрицательный, то вся дробь отрицательная.
3. Неправильная дробь и смешанная дробь. Неправильная дробь – это дробь, у которой числитель больше знаменателя. Смешанная дробь – это сумма целой части и правильной дроби. Например, 3 1/4 – это смешанная дробь, где 3 – целая часть, 1 – числитель и 4 – знаменатель.
4. Операции с дробями. Дроби можно складывать, вычитать, умножать и делить. При сложении или вычитании дробей их знаменатели должны быть одинаковыми. При умножении дробей числитель одной дроби умножается на числитель другой дроби, а знаменатель – на знаменатель. При делении одну дробь нужно умножить на обратную к дроби.
5. Упрощение дробей. Дробь можно упростить, если числитель и знаменатель делятся на одно и то же число без остатка. Упрощение позволяет записать дробь в наименьших возможных значениях числителя и знаменателя.
Может ли числитель дроби быть равным 0?

Если числитель дроби равен нулю, то такая дробь называется нулевой дробью. Нулевая дробь обозначается символом 0/1 или просто 0. Но такая запись является частным случаем и имеет особую семантику.
Нулевая дробь не может иметь определенного численного значения, так как не определен делитель, равный нулю. В математике считается, что деление на ноль не определено и не имеет смысла. Поэтому, если числитель дроби равен нулю, то вся дробь также равна нулю.
Другими словами, можно сказать, что нулевая дробь является исключением из общего правила, а необычным случаем любой дроби. Числитель дроби не может быть равным нулю в общем случае, исключение составляет только случай нулевой дроби.
Учитывая это, важно помнить, что при решении математических задач и вычислениях следует исключать нулевые дроби, поскольку они не имеют определенного значения и могут привести к некорректным результатам.
Исследуем случай с числителем равным 0
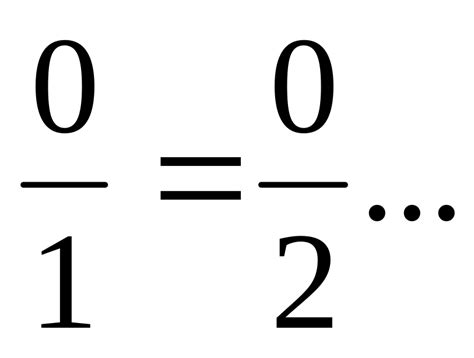
При рассмотрении дробей, важно исследовать случай, когда числитель равен 0. Для этого рассмотрим уравнение:
0/3 = 0
Уравнение показывает, что дробь с нулевым числителем равна нулю. Это связано с тем, что если числитель равен нулю, то вся дробь будет равна нулю, независимо от значения знаменателя.
Какие примеры дробей с числителем 0 можно найти?

В математике, дробью называется отношение двух чисел, числителя и знаменателя. Числитель обозначает количество, которое мы хотим взять из некоторого целого или числа, а знаменатель обозначает, на сколько частей мы делим это число. Когда числитель равен 0, мы получаем дробь, в которой количество берется из нуля.
Один из примеров дроби с числителем 0 - это дробь 0/1. В этом случае, числитель равен 0, что означает, что мы не берем никакое количество. Знаменатель равен 1, что означает, что мы делим некоторое число на одну равную часть.
Еще один пример - это дробь 0/2. В этом случае, числитель также равен 0, но знаменатель равен 2, что означает, что мы делим некоторое число на две равные части. Результатом будет 0, так как мы не берем никакое количество из него.
Дроби с числителем 0 можно находить и в других случаях. Например, дробь 0/3 означает, что мы делим некоторое число на три равные части, но не берем никакое количество из него.
Таким образом, можно сказать, что дробь с числителем 0 означает, что мы не берем никакое количество из некоторого числа при разделении его на равные части.
Что происходит при делении на ноль?

Арифметические правила определяют деление на ноль как деление на ноль из ненулевого числа. Такая операция считается некорректной и неопределенной. Она противоречит основным принципам алгебры и многих других математических дисциплин.
При попытке выполнить деление на ноль возникает ошибка, которая может привести к остановке программы или появлению сообщения об ошибке. Это связано с тем, что деление на ноль не имеет смысла и приводит к некорректным результатам.
В некоторых математических областях, таких как теория пределов или теория меры, существуют понятия, приближающие деление на ноль. Например, предел функции, стремящейся к нулю, может быть определен и изучен при анализе различных предельных условий.
Однако в обычной арифметике и большинстве применений численных вычислений деление на ноль не имеет смысла и не представляет интереса.
Рассматриваем деление на ноль
Однако, когда мы рассматриваем дроби, вопрос о делении на ноль может возникнуть. Допустим, у нас есть дробь с числителем равным нулю: 0/м, где м - ненулевое число. Что будет в этом случае?
При делении числа на ноль, результатом будет либо бесконечность (положительная или отрицательная), либо неопределенность. Это называется предельным значением. То есть, 0/м будет равно 0, но также будет стремиться к бесконечности при меньшей величине м.
Таким образом, можно сказать, что дробь с числителем 0 имеет специфическое предельное значение при делении на ненулевое число. Однако, в реальном мире, деление на ноль остается невозможным и не имеет четкого значения.
| Деление | Результат |
|---|---|
| 0/м (м ≠ 0) | 0 (предельное значение) |
| 0/0 | неопределенность |



