Концепция принадлежности точки плоскости позволяет определить, лежит ли данная точка на заданной плоскости или находится вне ее. Для этого необходимо учитывать различные математические правила, которые позволяют определить, является ли точка частью плоскости или нет.
Основное правило для определения принадлежности точки плоскости заключается в том, что координаты точки должны удовлетворять уравнению плоскости. Уравнение плоскости представляет собой линейное уравнение, в котором содержатся координаты точек плоскости и коэффициенты, определяющие ее положение и форму.
Например, уравнение плоскости может быть представлено в виде: Ax + By + Cz + D = 0, где A, B, C и D - это числовые значения, а x, y и z - координаты точки.
Для лучшего понимания концепции принадлежности точки плоскости можно рассмотреть пример. Предположим, что задана плоскость с уравнением 2x - 3y + z - 4 = 0. Для определения принадлежности точки (1, 2, 3) плоскости, необходимо подставить ее координаты в уравнение и выполнить вычисления.
2 * 1 - 3 * 2 + 3 - 4 = 2 - 6 + 3 - 4 = -5.
Так как результат не равен нулю, это означает, что точка (1, 2, 3) не принадлежит заданной плоскости.
Таким образом, основная идея принадлежности точки плоскости состоит в том, чтобы подставить координаты точки в уравнение плоскости и проверить, равен ли результат нулю. Если равен, то точка принадлежит плоскости, если не равен - точка не принадлежит плоскости.
Точка принадлежит плоскости только в том случае

Чтобы установить, принадлежит ли точка плоскости, необходимо выполнение следующих условий:
- Уравнение плоскости должно быть задано (в виде уравнения вида: Ax + By + Cz + D = 0), где A, B и C - коэффициенты, а x, y и z - координаты точки.
- Подставьте координаты точки в уравнение плоскости и получите уравнение вида: Ax + By + Cz + D = значение. Полученное значение должно равняться нулю, чтобы точка принадлежала плоскости.
Например, если дано уравнение плоскости 3x + 2y - 5z + 7 = 0 и координаты точки (1, 2, -1), мы можем подставить их в уравнение:
3 * 1 + 2 * 2 - 5 * (-1) + 7 = 3 + 4 + 5 + 7 = 19.
Значение равно 19, а не нулю, поэтому точка (1, 2, -1) не принадлежит заданной плоскости.
Что такое плоскость и точка

Точка – это элементарный объект геометрии, который не имеет никаких измеримых размеров. Точка обозначается буквой, например, как "А".
Чтобы определить, принадлежит ли точка плоскости, необходимо проверить выполнение определенных правил:
- Правило 1: Координаты точки - задайте координаты точки в пространстве. Плоскость задается уравнением, и для включения точки в плоскость ее координаты должны удовлетворять этому уравнению.
- Правило 2: Основные свойства - убедитесь, что заданная точка лежит на прямых, проходящих через плоскость. Если прямые, проходящие через точку, также проходят через плоскость, то точка принадлежит плоскости.
Например, рассмотрим плоскость, заданную уравнением 2x + 3y - z = 6 и точку А с координатами (1, 2, -1). Подставляем координаты точки в уравнение плоскости: 2 * 1 + 3 * 2 - (-1) = 6. Получаем верное равенство, следовательно, точка А принадлежит плоскости.
Основные правила определения принадлежности точки плоскости

Для определения принадлежности точки плоскости нужно учитывать несколько основных правил и условий.
1. Плоскость задается уравнением вида Ax + By + Cz + D = 0, где A, B, C и D - это коэффициенты уравнения, а x, y и z - координаты точки плоскости.
2. Если подставить значения координат точки в уравнение плоскости и получится нулевое значение, то точка принадлежит плоскости. Если результат отличен от нуля, то точка не принадлежит плоскости.
3. Нулевая точка координат (0, 0, 0) всегда принадлежит любой плоскости, так как она удовлетворяет уравнению плоскости.
4. Если плоскость задана векторами, то точка принадлежит плоскости, если она лежит на плоскости, определенной этими векторами.
Примеры:
1. Для плоскости 2x - 3y + z - 5 = 0 и точки (3, -1, 4):
2 * 3 + (-3) * (-1) + 1 * 4 - 5 = 0 + 3 + 4 - 5 = 2 + 2 = 4
Результат не равен нулю, значит точка (3, -1, 4) не принадлежит плоскости.
2. Для плоскости x + y + z = 6 и точки (1, 2, 3):
1 + 2 + 3 = 6
Результат равен нулю, значит точка (1, 2, 3) принадлежит плоскости.
Уравнение плоскости в пространстве

Уравнение плоскости в трехмерном пространстве задается общим видом:
Ax + By + Cz + D = 0
где A, B, C - коэффициенты, определяющие нормаль к плоскости, а D - свободный член.
Коэффициенты A, B, C определяются координатами вектора, перпендикулярного плоскости. Например, если даны три точки принадлежащие плоскости (x1, y1, z1), (x2, y2, z2) и (x3, y3, z3), то вектор нормали можно найти по следующей формуле:
N = (x2 - x1, y2 - y1, z2 - z1) × (x3 - x1, y3 - y1, z3 - z1)
где × обозначает векторное произведение. Коэффициенты A, B, C равны соответствующим координатам найденного вектора.
Уравнение плоскости можно использовать, чтобы проверить, принадлежит ли точка заданной плоскости. Для этого нужно подставить координаты точки (x, y, z) в уравнение плоскости и проверить, что получается равенство:
Ax + By + Cz + D = 0
Если равенство выполняется, то точка принадлежит плоскости, иначе - нет.
Например, у нас есть плоскость с уравнением 3x + 2y - z + 5 = 0. Чтобы проверить, принадлежит ли точка (1, -2, 3) этой плоскости, нужно подставить ее координаты в уравнение:
3*1 + 2*(-2) - 3 + 5 = 3 - 4 - 3 + 5 = 1
Так как получается равенство, то точка (1, -2, 3) принадлежит плоскости.
Координаты точек и их принадлежность к плоскости
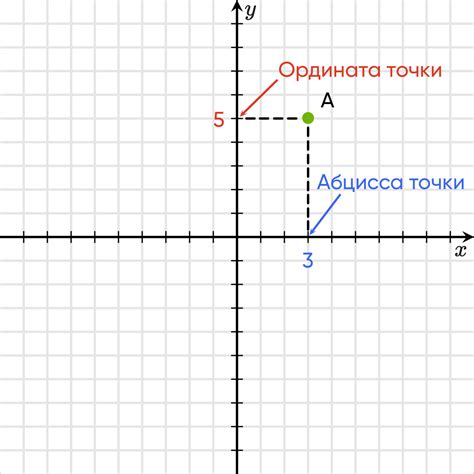
Координаты точек играют важную роль в геометрии и математике. Они помогают определить положение точки в пространстве и выяснить, принадлежит ли она заданной плоскости. Для того чтобы понять, принадлежит ли точка плоскости, необходимо использовать основные правила и примеры.
Для начала, давайте вспомним, что плоскость - это двумерная геометрическая фигура, которая не имеет объема. Она состоит из бесконечного числа точек и может быть определена с помощью трех координатных осей - оси X, Y и Z.
Если известны координаты точки и уравнение плоскости, то можно определить, принадлежит ли точка плоскости. Для этого необходимо подставить значения координат точки в уравнение плоскости и выполнить соответствующие математические операции.
Например, пусть у нас есть плоскость с уравнением: 2x + 3y - z = 6. Чтобы определить, принадлежит ли точка (1, 2, 3) этой плоскости, необходимо подставить значения координат точки в уравнение:
- Подставляем x = 1, y = 2 и z = 3 в уравнение плоскости: 2*1 + 3*2 - 3 = 6
- Выполняем математические операции: 2 + 6 - 3 = 9
Так как результат не равен 6, значит, точка (1, 2, 3) не принадлежит данной плоскости.
Чтобы еще лучше понять механизм определения принадлежности точки к плоскости, рассмотрим другой пример:
- У нас есть плоскость с уравнением: x - 3y + 2z = 7
- Определяем координаты точки, например, (4, 1, 2)
- Подставляем значения координат точки в уравнение плоскости: 4 - 3*1 + 2*2 = 7
- Выполняем математические операции: 4 - 3 + 4 = 7
Так как результат равен 7, значит, точка (4, 1, 2) принадлежит данной плоскости.
Итак, зная координаты точки и уравнение плоскости, можно определить, принадлежит ли точка заданной плоскости, подставив значения координат в уравнение и выполнить соответствующие математические операции.
Геометрическое определение принадлежности точки плоскости

Для определения принадлежности точки плоскости необходимо учесть, что плоскость можно представить в виде таблицы с координатами точек, принадлежащих ей. Исходя из этого, можно сформулировать следующие основные правила:
| Правило | Описание | Пример |
|---|---|---|
| 1 | Если координаты точки совпадают с координатами любой точки плоскости, то данная точка принадлежит этой плоскости. | Точка A(2, 3, 4) принадлежит плоскости АВСD с координатами ABCD(2, 3, 4), (1, 2, 3), (4, 5, 6), (7, 8, 9). |
| 2 | Если координаты точки удовлетворяют уравнению плоскости, то данная точка принадлежит этой плоскости. | Точка B(1, -2, 3) принадлежит плоскости Ax + By + Cz + D = 0, где A = 2, B = -1, C = 3, D = 5. |
| 3 | Если координаты точки образуют прямую линию с двумя другими точками плоскости, то данная точка принадлежит этой плоскости. | Точка С(0, 1, 2) принадлежит плоскости ABC с координатами A(1, 2, 3), B(2, 3, 4), C(0, 1, 2). |
Учет этих основных правил позволяет определить принадлежность точки плоскости в геометрическом смысле и представить результат в виде таблицы с примерами.
Теорема о принадлежности точки плоскости

Уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C - это коэффициенты, определяющие нормальный вектор плоскости, а x, y, z - координаты точки. Также важно отметить, что A, B и C не могут быть одновременно равными нулю, чтобы плоскость имела определенное положение в пространстве.
Для определения принадлежности точки плоскости нужно подставить ее координаты в уравнение плоскости. Если после подстановки получится равенство, то точка принадлежит плоскости, если нет, то точка не принадлежит плоскости.
В таблице ниже приведены примеры принадлежности точек плоскости:
| Точка | Уравнение плоскости | Результат |
|---|---|---|
| (1, 2, 3) | 2x + 3y + 4z - 10 = 0 | Принадлежит |
| (-1, 5, 2) | 2x + 3y + 4z - 10 = 0 | Не принадлежит |
| (0, 0, 0) | 2x + 3y + 4z - 10 = 0 | Не принадлежит |
Теорема о принадлежности точки плоскости является важным инструментом в геометрии и находит свое применение в различных областях, например, в астрономии, физике и графике компьютерной графики.
Примеры определения принадлежности точек к плоскости
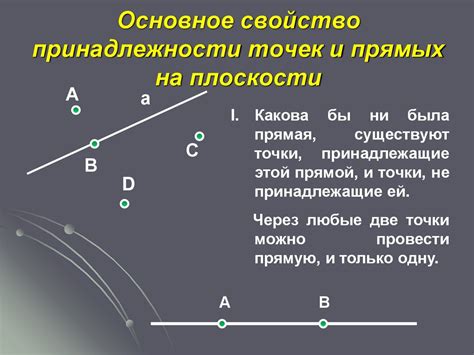
Принадлежность точки к плоскости можно определить, рассчитав ее координаты и подставив их в уравнение плоскости. Если после подстановки получается равенство, то точка лежит на данной плоскости.
Рассмотрим несколько примеров:
Уравнение плоскости: 2x + 3y - z = 7
Точка A(1, 2, 3)
Подставляем координаты точки в уравнение: 2*1 + 3*2 - 3 = 2 + 6 - 3 = 5
Получили 5, что не равно 7. Значит, точка A не принадлежит данной плоскости.
Уравнение плоскости: x - 2y + z = -4
Точка B(0, -2, -6)
Подставляем координаты точки в уравнение: 0 - 2*(-2) - 6 = 0 + 4 - 6 = -2
Получили -2, что равно -4. Значит, точка B принадлежит данной плоскости.
Уравнение плоскости: 3x + 2y - 4z = 0
Точка C(-2, 1, 1)
Подставляем координаты точки в уравнение: 3*(-2) + 2*1 - 4*1 = -6 + 2 - 4 = -8
Получили -8, что не равно 0. Значит, точка C не принадлежит данной плоскости.
Таким образом, определение принадлежности точек к плоскости сводится к подстановке их координат в уравнение плоскости и проверке полученного равенства.



