Теорема Пифагора – это одна из величайших и наиболее известных теорем в математике. Она устанавливает взаимосвязь между длинами сторон прямоугольного треугольника. Как известно, для прямоугольного треугольника с катетами a и b и гипотенузой c выполняется следующее равенство: a² + b² = c².
Однако в некоторых случаях в теореме Пифагора может применяться отрицательное значение. Это происходит, когда одна из сторон треугольника отрицательна по длине. В таких ситуациях, равенство принимает вид: a² + b² = -c².
Например, рассмотрим треугольник, у которого одна сторона имеет длину -3. В этом случае, используя отрицательное значение, можно применить теорему Пифагора и найти длины остальных сторон. В результате получим: (-3)² + b² = c². Затем, проведя вычисления, можно найти значения b и c.
Отрицательное значение в теореме Пифагора имеет своеобразное применение и может быть полезным в некоторых математических и физических задачах. Однако в большинстве случаев, при решении проблем, связанных с геометрией или физикой, используются только положительные значения длин сторон треугольника.
Отрицательное значение в теореме Пифагора
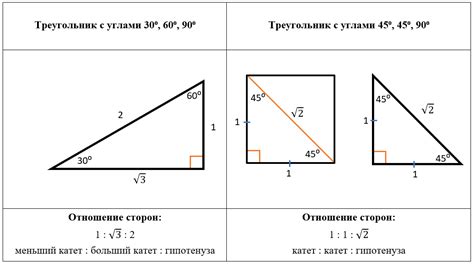
В обычной формулировке теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это можно записать следующей формулой:
c² = a² + b²
Где c - длина гипотенузы, а и b - длины катетов треугольника.
Однако, в некоторых случаях, вместо положительного значения длины, теорема Пифагора дает отрицательный результат. Это может произойти, если ошибочно выбран знак одного из катетов или гипотенузы.
Отрицательное значение в теореме Пифагора может указывать на ошибку в расчетах или на невозможность построить прямоугольный треугольник с заданными длинами сторон.
Например, если в прямоугольном треугольнике длина гипотенузы равна 5, а длины катетов равны 3 и -4, то результат будет отрицательным:
5² = 3² + (-4)²
25 = 9 + 16
25 ≠ 25
В этом случае возникает противоречие, и теорема Пифагора не выполняется.
Поэтому при использовании теоремы Пифагора необходимо правильно выбирать знаки длин сторон треугольника и следить за правильностью расчетов. В случае отрицательного значения, нужно перепроверить данные и убедиться в их правильности.
Как можно использовать отрицательное значение в теореме Пифагора?

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Обычно все длины, используемые в теореме, считаются положительными числами. Однако, существуют ситуации, когда можно использовать отрицательное значение в теореме Пифагора.
В первую очередь, отрицательные значения могут быть использованы, когда рассматривается не прямоугольный, а обобщенный треугольник. Например, в сферической геометрии, где треугольники могут быть не плоскими, отрицательные значения могут возникать при измерении углов и сторон треугольника. В таких случаях, теорему Пифагора можно применить, но нужно учесть, что квадраты длин сторон могут быть отрицательными.
Кроме того, отрицательные значения могут возникать, когда рассматривается векторная форма теоремы Пифагора. Векторы могут иметь не только положительные, но и отрицательные компоненты. Например, при сложении двух векторов с противоположными направлениями, длина результирующего вектора может быть отрицательной. Однако, при использовании теоремы Пифагора векторного суммирования, нужно учитывать и направление векторов.
Когда может быть применена отрицательная формула теоремы Пифагора?

Теорема Пифагора, которая устанавливает соотношение между длинами сторон прямоугольного треугольника, обычно представляется в виде положительной формулы:
a2 + b2 = c2
где a и b - длины катетов, а c - длина гипотенузы треугольника.
Однако, иногда встречаются случаи, когда необходимо применение отрицательной формулы теоремы Пифагора. Такое может случиться, если одна из сторон треугольника имеет отрицательную длину или когда треугольник расположен в пространстве с отрицательной кривизной.
Например, в геометрии на сфере, где пространство имеет положительную кривизну, отрицательная формула теоремы Пифагора применяется для вычисления длины дуги геодезической линии (например, большого круга) на сфере. Это позволяет учесть отрицательное значение некоторых параметров и получить корректный результат.
Необходимость применения отрицательной формулы теоремы Пифагора также может возникнуть в некоторых областях физики и математики, где могут возникать отрицательные значения длин или других величин.
Важно отметить, что отрицательная формула теоремы Пифагора не противоречит основным принципам и свойствам треугольников, но ее применение обуславливается специфическими условиями задачи или контекстом, в котором применяется.



