</p>
Системы неравенств являются одним из важных инструментов математического анализа и используются для решения широкого спектра задач. Знание правил изменения знака в системе неравенств позволяет корректно проводить необходимые операции и получать верные результаты.
Основное правило изменения знака в системе неравенств заключается в том, что когда умножается или делится обе части неравенства на отрицательное число, то знаки неравенства изменяются на противоположные. То есть, если у нас есть неравенство a < b, где a и b - положительные числа, и мы делим обе части на отрицательное число c, то получим неравенство -a/c > -b/c.
Важно учитывать, что если у нас есть неравенство a > b и мы умножаем обе части на отрицательное число c, то неравенство меняет свой знак на противоположный. В результате мы получим неравенство -a < -b. Это правило позволяет вести корректные вычисления и использовать системы неравенств в различных сферах науки и техники.
Знаки в системе неравенств: важные тонкости
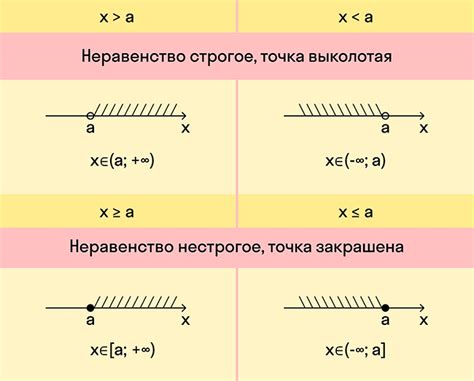
Основные знаки системы неравенств:
- Знак «больше» (>) указывает, что одно число больше другого. Например, 5 > 3 означает, что 5 больше 3.
- Знак «меньше» (<) указывает, что одно число меньше другого. Например, 2 < 7 означает, что 2 меньше 7.
- Знак «больше или равно» (≥) указывает, что одно число больше или равно другому. Например, 4 ≥ 4 означает, что 4 больше или равно 4.
- Знак «меньше или равно» (≤) указывает, что одно число меньше или равно другому. Например, 6 ≤ 9 означает, что 6 меньше или равно 9.
Когда выполняются операции с системой неравенств, знак в системе может изменяться в зависимости от операции.
Например, при умножении или делении обе стороны неравенства на отрицательное число, знак неравенства меняется на противоположный:
- Если a > b и c < 0, то ac < bc.
- Если a < b и c < 0, то ac > bc.
При сложении или вычитании одного и того же числа с обеих сторон неравенства, знак неравенства не меняется:
- Если a > b, то a + c > b + c.
- Если a < b, то a - c < b - c.
Важно знать эти тонкости для правильного решения и обработки систем неравенств. Использование правильных знаков позволит избегать ошибок и получать точные ответы.
Переход через ноль: критический момент для знака
Когда значение переменной достигает нуля, возникает возможность изменения знака. В случае, если переменная была положительной и при переходе через ноль становится отрицательной, знак неравенства меняется с «больше» на «меньше». Если же переменная была отрицательной и становится положительной при переходе через ноль, знак неравенства меняется на противоположный, с «меньше» на «больше».
Таким образом, переход через ноль предоставляет нам важную информацию о характере неравенства. Благодаря этому критическому моменту, мы можем определить, в какой области значений переменной выполняется неравенство и каким образом оно связано с осью чисел.
Действия с обоими частями неравенств

При изменении знака в системе неравенств, важно учесть, что обе части неравенства должны оставаться неизменными. Это означает, что действия, которые мы выполняем с одной частью, должны также быть выполнены с другой частью. В этом разделе мы рассмотрим основные действия с обоими частями неравенств.
1. Сложение или вычитание числа: Если мы сложим или вычтем одно и то же число из обеих частей неравенства, знак неравенства останется таким же. Например, если у нас есть неравенство "а < b" и мы добавляем или вычитаем число "с" из обеих частей, то новое неравенство будет выглядеть так: "а + с < b + с" или "а - с < b - с".
2. Умножение или деление на положительное число: Если мы умножаем или делим обе части неравенства на положительное число, знак неравенства останется таким же. Например, если у нас есть неравенство "а < b" и мы умножаем или делим обе части на положительное число "с", то новое неравенство будет выглядеть так: "а * с < b * с" или "а / с < b / с".
3. Умножение или деление на отрицательное число: Если мы умножаем или делим обе части неравенства на отрицательное число, знак неравенства меняется на противоположный. Например, если у нас есть неравенство "а < b" и мы умножаем или делим обе части на отрицательное число "с", то новое неравенство будет выглядеть как: "а * с > b * с" или "а / с > b / с".
Важно помнить, что при выполнении действий с обоими частями неравенства нужно быть внимательными и не перепутать знаки, так как это может привести к неправильному результату.
На пути к новому знаку: примеры и упражнения

Для того чтобы лучше понять, когда меняется знак в системе неравенств, рассмотрим несколько примеров и выполним несколько упражнений.
| Пример | Условие | Знак |
|---|---|---|
| Пример 1 | x + 3 > 5 | > |
| Пример 2 | 2y - 4 ≤ 10 | ≤ |
| Пример 3 | 4z + 2 < 6 | < |
Давайте решим первый пример:
Нам дано уравнение x + 3 > 5. Чтобы найти значение переменной x, нужно из 5 вычесть 3. Получаем x > 2.
Итак, в первом примере знак неравенства меняется на >.
Теперь давайте попробуем выполнить несколько упражнений, чтобы укрепить полученные знания.
Упражнение 1:
Решите неравенство 2a + 6 ≥ 10.
Вам нужно найти значение переменной a так, чтобы условие было истинным. В данном случае надо из 10 вычесть 6, получим 2a ≥ 4. Значит, a ≥ 2.
Упражнение 2:
Решите неравенство 3b - 5 < 7.
В данном примере нужно найти значение переменной b так, чтобы неравенство было истинным. Добавляем 5 к обеим сторонам неравенства и получаем 3b < 12. Значит, b < 4.
Продолжайте выполнять подобные упражнения, чтобы научиться определять, когда меняется знак в системе неравенств. Практика - это ключ к успеху!



