Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине. В связи с этим, многие люди задаются вопросом: верно ли, что в любом параллелограмме диагонали равны?
Диагональ - это отрезок, соединяющий две вершины четырехугольника, которые не являются соседними. В параллелограмме есть две диагонали: одна соединяет вершины, лежащие на противоположных сторонах, а другая – вершины, лежащие на других противоположных сторонах.
Однако, не все параллелограммы обладают свойством равенства диагоналей. Между тем, есть тип параллелограммов, в которых диагонали равны. Этим типом является прямоугольник. В прямоугольнике противоположные стороны не только параллельны и равны, но и перпендикулярны друг другу. Это свойство приводит к тому, что диагонали прямоугольника также оказываются равными.
В остальных случаях, когда речь идет о параллелограммах, диагонали обычно не равны, так как обладают разными углами и длинами сторон. Параллелограмм может быть с несимметричными сторонами и углами, и это влияет на длины его диагоналей. Например, в ромбе, который является видом параллелограмма, диагонали также равны, но они пересекаются под прямым углом.
Определение параллелограмма

Чтобы лучше представить себе параллелограмм, можно рассмотреть его основные элементы. Стороны параллелограмма - это отрезки, соединяющие вершины фигуры. Диагонали параллелограмма - это отрезки, соединяющие противоположные вершины. Каждая диагональ параллелограмма делит его на два треугольника, которые могут быть различными: прямоугольными, остроугольными или тупоугольными.
Для параллелограмма характерны следующие свойства:
| Стороны | Противоположные стороны параллельны и равны. |
| Углы | Противоположные углы параллелограмма равны. |
| Диагонали | Диагонали параллелограмма делят его на два равных треугольника. |
Таким образом, параллелограмм – это особый тип четырехугольника, который обладает несколькими уникальными свойствами. Знание этих свойств поможет лучше понять его структуру и поведение.
Изучение структуры фигуры
Стороны: Параллелограмм имеет две пары равных и параллельных сторон. Каждая пара сторон параллельна и одинаково удалена друг от друга. Боковые стороны параллелограмма расположены попарно противоположно друг другу.
Углы: Параллелограмм имеет две пары равных углов. Углы, расположенные попарно противоположно друг другу, являются равными. Сумма всех углов в параллелограмме равна 360 градусов.
Диагонали: Диагонали параллелограмма соединяют противоположные вершины. Диагонали внутри параллелограмма пересекаются в точке, называемой центром. Диагонали равны по длине, то есть отрезки, соединяющие центр с вершинами параллелограмма, равны между собой.
Таким образом, ответ на вопрос, верно ли, что в любом параллелограмме диагонали равны, будет утвердительным. Диагонали параллелограмма всегда равны между собой и пересекаются в центре фигуры.
Свойства параллелограмма
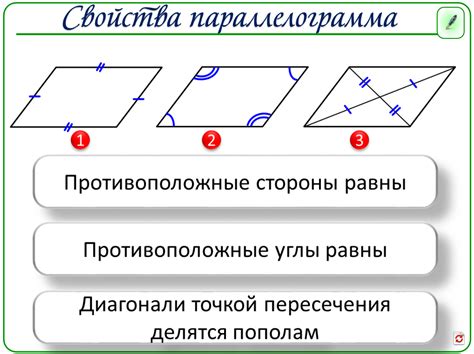
В параллелограмме существуют несколько важных свойств:
1. Равные противоположные стороны: Все стороны параллелограмма равны попарно. Это свойство обусловлено тем, что противоположные стороны параллельны и поэтому имеют одинаковую длину.
2. Равные противоположные углы: Углы между параллельными сторонами параллелограмма также равны попарно. Это следует из свойств параллельных линий, которые формируются при пересечении диагоналей параллелограмма.
3. Противоположные стороны параллельны: Это основное свойство параллелограмма. Параллельность сторон позволяет параллелограмму быть фигурой, у которой противоположные стороны параллельны и равны по длине.
4. Диагонали делятся пополам: Диагонали параллелограмма делят друг друга пополам. То есть, точка их пересечения является серединой их длины. Это свойство следует из параллельности сторон и задает специфическую структуру параллелограмма.
Из этих свойств можно вывести еще много других. Они позволяют определить разные параметры параллелограмма и решать разнообразные задачи, связанные с этой фигурой.
Равенство противоположных сторон

В параллелограмме определены две пары противоположных сторон. Каждая пара состоит из двух сторон, которые расположены напротив друг друга и параллельны между собой. Одна из особенностей параллелограмма заключается в том, что противоположные стороны имеют одинаковую длину.
Равенство противоположных сторон является следствием особенности параллелограмма – его параллельных сторон. Параллельные стороны имеют одинаковую длину, поэтому противоположные стороны тоже должны быть равными. Это можно легко доказать с помощью геометрических свойств параллелограмма.
Равенство противоположных сторон является одним из ключевых свойств параллелограмма. Благодаря этому свойству параллелограммы имеют ряд уникальных характеристик и связанных с ними формул и теорем, которые используются в геометрии.
Равенство диагоналей в параллелограмме
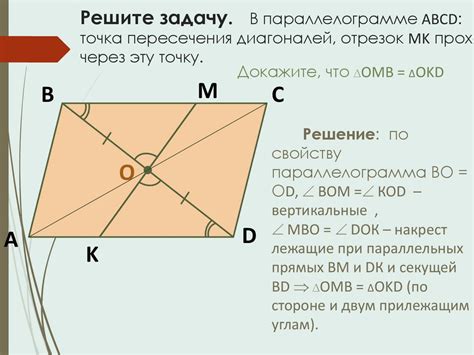
Диагональ - это отрезок, соединяющий вершины, не являющиеся соседними.
Если рассматривать параллелограмм, то его диагонали - это отрезки, соединяющие противоположные вершины.
Верно ли, что в любом параллелограмме диагонали равны? Ответ - да.
Доказательство равенства диагоналей в параллелограмме можно провести с помощью сходства треугольников или с помощью использования свойств параллелограмма.
Сходство треугольников позволяет установить, что в параллелограмме диагонали делятся пополам. Это означает, что диагонали равны.
Свойства параллелограмма подтверждают, что противоположные стороны равны и параллельны. Таким образом, диагонали параллелограмма также равны.
Доказательство равенства диагоналей
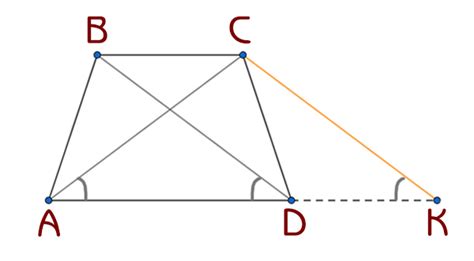
В любом параллелограмме диагонали, соединяющие противоположные вершины, равны между собой. Для доказательства этого факта рассмотрим параллелограмм ABCD.
Рисунок:
A _________________ B / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / D -/
Проведем диагонали AC и BD. Они пересекаются в точке O.
Рисунок:
A _____________ B / / | / / | / / | / / | / / | / / | / / | / / | / / | / / | / / | / / | / / | / / | / / | / / | D -/ | | | O |_________________|
Треугольники AOB и COD по построению являются равнобедренными, так как AC = BD (диагонали параллелограмма).
В этих треугольниках AO = OC, BO = OD, так как это равные отрезки (по построению).
Таким образом, треугольники AOB и COD равны по двум сторонам и углу. Значит, они подобны.
Из подобия треугольников следует, что углы AOB и COD равны. Но угол AOB равен углу COD, так как они являются вертикальными (по определению вертикальных углов).
Значит, углы AOC и BOD равны.
Таким образом, треугольники AOC и BOD равны по двум сторонам и углу. Значит, они подобны.
Из подобия треугольников следует, что стороны OC и OD пропорциональны сторонам AO и BO, соответственно.
Но AO = OC и BO = OD, так как это равные отрезки (по построению).
Значит, OC = OD, то есть диагонали AC и BD равны между собой.



