Закон многоугольника для векторов является важным понятием в линейной алгебре и находит широкое применение в различных областях знаний. Этот закон описывает свойства векторов, их сложение и отношения между ними. Закон многоугольника основывается на принципе, что вектор может быть представлен как сумма нескольких других векторов, начиная с определенной точки.
Одним из основных правил закона многоугольника является то, что сумма векторов, исходящих из одной точки и образующих замкнутый многоугольник, равна нулевому вектору. Это означает, что если мы возьмем несколько векторов, начинающихся из одной точки и сложим их, то получим нулевой вектор.
Применение закона многоугольника для векторов помогает решать различные задачи в физике, геометрии, программировании и других науках. Например, в физике этот закон используется для определения равновесия сил, действующих на тело.
В данной статье мы рассмотрим несколько примеров, иллюстрирующих применение закона многоугольника для векторов. Мы узнаем, как использовать этот закон для решения задач и как он может помочь нам лучше понять свойства векторов.
Закон многоугольника для векторов с нулевым вектором: основные принципы

Основными принципами закона многоугольника для векторов с нулевым вектором являются:
- Сумма всех векторов, образующих замкнутый многоугольник, равна нулевому вектору.
- Вектор, соединяющий начало первого вектора с концом последнего вектора, является нулевым вектором.
- Координаты нулевого вектора равны 0 в каждом измерении.
Принципы закона многоугольника можно проиллюстрировать на примере:
- Пусть имеется треугольник ABC, где AB = вектор a, BC = вектор b и CA = вектор c. Если треугольник замкнутый (то есть точка A совпадает с точкой C), то сумма векторов a, b и c равна нулевому вектору.
- Если в треугольнике ABC точка A не совпадает с точкой C, то сумма векторов a, b и c будет вектором, соединяющим начало вектора a с концом вектора c.
Закон многоугольника для векторов с нулевым вектором полезен при решении различных задач, связанных с анализом векторных пространств. Он помогает определить результирующий вектор при сложении нескольких векторов и дает представление о равновесии сил в физических задачах.
Векторы и их свойства
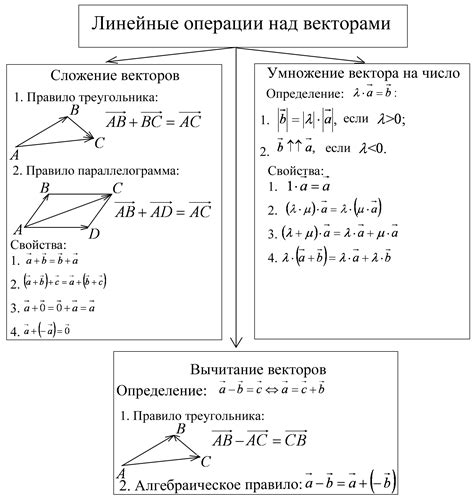
У векторов есть несколько основных свойств:
- Нулевой вектор: нулевой вектор представляет собой вектор, у которого все компоненты равны нулю. Он не имеет определенного направления и длины.
- Параллельность: векторы называются параллельными, если они имеют одинаковое направление или противоположное.
- Сложение векторов: сложение векторов производится покомпонентно. Компоненты соответствующих векторов складываются и образуют компоненты результирующего вектора.
- Умножение вектора на скаляр: умножение вектора на скаляр (число) производится покомпонентно. Каждая компонента вектора умножается на заданное число.
- Длина вектора: длина (модуль) вектора вычисляется с использованием теоремы Пифагора для многомерного пространства.
- Единичный вектор: единичный вектор – это вектор, длина которого равна единице. Он используется для определения направления вектора.
Знание свойств векторов является важной основой в математике, физике и компьютерной графике. Они позволяют выполнять различные операции с векторами и применять их в решении разнообразных задач.
Определение многоугольника для векторов

Многоугольник для векторов может быть составлен из различных типов векторов, таких как радиус-векторы, стороны многоугольника и диагонали. Длины и направления векторов определяют форму и положение многоугольника.
Для определения многоугольника для векторов необходимо знать координаты начальной точки и величину и направление каждого вектора, составляющего многоугольник. Векторы могут быть заданы векторным представлением или координатами начальной и конечной точек.
Используя закон многоугольника для векторов с нулевым вектором, можно определить свойства многоугольника, такие как периметр, площадь и углы между сторонами. Это позволяет проводить анализ и решать задачи, связанные с многоугольниками, с помощью векторных методов.
Правила применения закона многоугольника для векторов
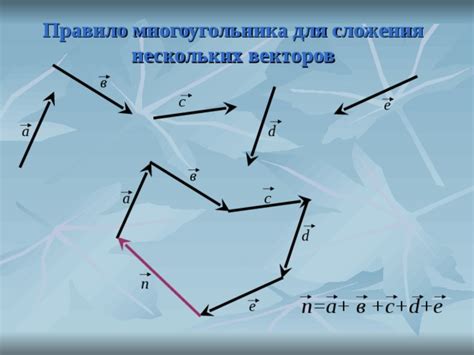
Основная идея закона многоугольника заключается в следующем: если мы имеем несколько векторов, которые начинаются в одной точке, мы можем замкнуть их в несколько многоугольников, где каждая сторона многоугольника соответствует вектору. Сумма всех этих векторов равна нулевому вектору.
У закона многоугольника для векторов есть несколько правил применения:
- Векторы должны начинаться и заканчиваться в одной точке.
- Векторы могут быть расположены в пространстве в любом порядке.
- Векторы, имеющие одинаковую длину и направление, могут быть заменены одним вектором с удвоенной длиной.
- Векторы, имеющие одинаковую длину, но противоположное направление, могут быть заменены нулевым вектором.
Например, у нас есть векторы A, B и C, которые начинаются в одной точке. Вектор A имеет длину 6 и направление 45 градусов, вектор B имеет длину 4 и направление 120 градусов, а вектор C имеет длину 2 и направление 270 градусов. Если мы замкнем эти векторы в многоугольник, то получим треугольник ABC. Согласно закону многоугольника, сумма этих векторов равна нулевому вектору.
Таким образом, закон многоугольника для векторов является мощным инструментом для вычисления суммы или разности нескольких векторов. Применение правил этого закона позволяет упростить вычисления и улучшить понимание результатов.
Сложение векторов по закону многоугольника
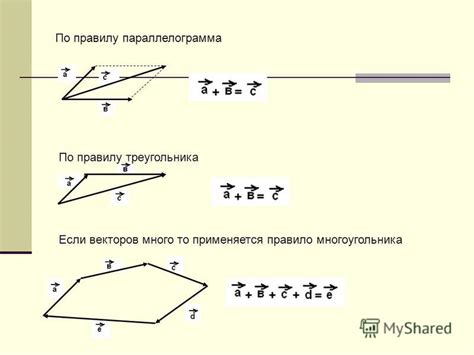
Закон многоугольника для векторов позволяет определить сумму двух или более векторов, используя геометрическое представление векторов.
Итак, пусть даны векторы а, б, с, ..., у с началом в общей точке O. Чтобы сложить эти векторы, нужно последовательно приложить их в концы друг за другом в том порядке, в котором они даны.
Для наглядности можно начать со сложения двух векторов а и б. Создадим параллелограмм, построенный на векторах а и б. Для этого проведем второй вектор б от конца первого вектора а.
Тогда диагональ полученного параллелограмма будет являться суммой векторов а и б. При этом направление суммы векторов совпадает с направлением последней диагонали.
Теперь, чтобы сложить еще один вектор с к сумме векторов а и б, проводим вектор с от конца суммы векторов и построим второй параллелограмм.
Третья диагональ полученного параллелограмма будет являться суммой векторов а, б и с. Продолжая этот процесс, можно приложить несколько векторов, и диагональ последнего параллелограмма будет являться искомой суммой векторов.
Таким образом, сложение векторов по закону многоугольника позволяет наглядно представить геометрическую сумму векторов и упрощает вычисления векторных операций.
Вычитание векторов по закону многоугольника
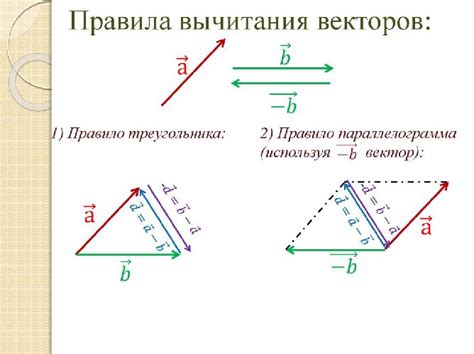
Правила вычитания векторов по закону многоугольника:
- Выберите два вектора, которые необходимо вычесть.
- Изначально расположите начало первого вектора в точке начала координат.
- Из точки начала первого вектора проведите луч в направлении второго вектора.
- При необходимости, сдвиньте начальную точку второго вектора так, чтобы он начинался с конца первого вектора.
- Постройте вектор, идущий от начала первого вектора до конца второго вектора.
- Получившийся вектор является разностью двух исходных векторов.
Пример вычитания векторов по закону многоугольника:
- Вектор A = (2, 3)
- Вектор B = (1, 2)
Вектор B нужно вычесть из вектора A:
- Начало вектора A в точке (0, 0).
- Проведем луч в направлении вектора B.
- Сдвинем начальную точку вектора B так, чтобы он начинался с конца вектора A.
- Построим вектор, идущий от начала вектора A до конца вектора B. Результат будет вектор C = (1, -1).
Таким образом, вычитание векторов по закону многоугольника позволяет найти разность двух векторов и использовать эту операцию для решения различных задач в физике, геометрии и других областях.



